The Time Value of Money (TVM)

Definition

The theory of time value suggests that money owned now is more valuable than the same amount of money owned in the future.

Example: The value of one unit of currency is higher now than in the future.

Reasons

1. Opportunity Cost: If you have one unit of currency now, you can immediately invest it, such as depositing it in a savings account or buying stocks, thereby making more money in the future. Therefore, the opportunity cost of forgoing the use of this unit of currency now is the potential of having more money in the future.
2. Inflation: As time goes by, prices usually rise, meaning that the same unit of currency will likely buy fewer goods or services in the future than it does now. Therefore, from the perspective of purchasing power, a unit of currency is more valuable now than in the future.
3. Risk and Uncertainty: The future is always filled with uncertainty. For example, the company you invest in may go bankrupt, or the person who borrows from you may fail to repay. Therefore, from the perspective of risk, a unit of currency now is more valuable than a unit of currency in the future.

Simple Interest

Definition

Simple interest refers to the situation where the interest of an investment or a loan is only calculated based on the initial principal and does not take into account the previously accumulated interest.

Characteristics

1. This means that the interest on the investment or debt is the same in each period.
2. The investment return (or debt cost) grows linearly with time, unlike compound interest, which grows exponentially over time.

Formula

The formula for simple interest is:

$$
FV = PV \times (1 + r \times t)
$$
Where:

• FV is the future value.
• PV is the present value, i.e., the principal of the investment.
• r is the annual interest rate.
• t is the number of years – it does not have to be an integer.

This formula indicates that the future value of the investment is the principal times (1 plus the annual interest rate times the number of years). The product of the annual interest rate and the number of years represents the total interest, and adding 1 means the principal plus interest.

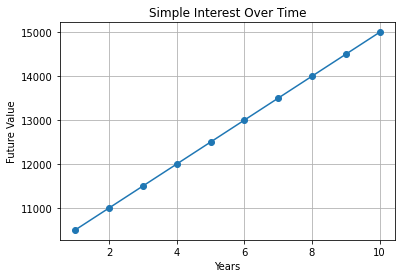
Example

If you deposit 10,000 units of currency, the annual interest rate is 5%, and the deposit is for 5 years, the future value can be calculated as follows:

PV = 10000 # Principal
r = 0.05 # Annual interest rate
t = 5 # Number of years

FV = PV (1 + r t)
= 10000 (1 + 0.05 5)
= 10000 * (1 + 0.25)
= 12500

Compound Interest

Definition

Compound interest is the interest that is generated not only on the principal but also on the accumulated interest.

Characteristics

1. Compound interest is calculated based on the principal and the interest that has already been generated.
2. Due to the generation of interest on interest, the investment return or debt cost grows exponentially over time, rather than linearly.

Formula

The formula for compound interest is:

$$
FV = PV \times \left(1 + \frac{r}{n}\right)^{nt}
$$

Where:

• FV is the future value.
• PV is the present value, i.e., the principal of the investment.
• r is the annual interest rate.
• n is the number of compounding periods per year.
• t is the number of years – it does not have to be an integer.

Example

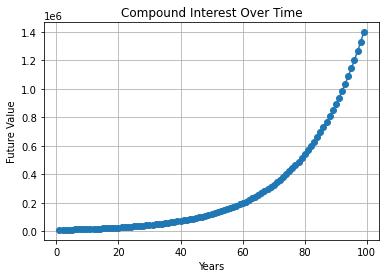
For example, if you deposit 10,000 units of currency, the annual interest rate is 5%, the deposit is for 5 years, and the interest is calculated 4 times a year (once a quarter), the future value can be calculated as follows:

PV = 10000 # Principal
r = 0.05 # Annual interest rate
t = 5 # Number of years
n = 4 # Number of compounding periods per year

FV = 10000 (1 + 0.05/4)^(45)
= 10000 * (1 + 0.0125)^(20)
= 12820.37

Annual Interest Rate

Background Knowledge: Multiple Compounding Periods

Financial products can compound multiple times within a year – for example, if interest is compounded twice a year (semi-annually), the annual interest rate is divided by 2, and interest is calculated every half year.

If interest is compounded four times a year (quarterly), the annual interest rate is divided by 4, and interest is calculated every quarter. This is called quarterly compounding.

Nominal Annual Interest Rate

The nominal annual interest rate, also known as the stated or face annual interest rate, is the basic annual interest rate that does not take into account the effect of compounding. This rate is usually the initial quoted interest rate for a loan or investment and does not take into account the impact of interest generating interest over the compounding period.

For example, if your savings account has a 2% nominal annual interest rate, this means that if you deposit for one year, without considering any compounding, you will receive interest equal to 2% of your deposit.

This is the most commonly used quotation method by financial institutions because it is easy to understand and calculate.

Effective Annual Interest Rate

The effective annual interest rate, or the effective annual rate (EAR), is the annual interest rate that takes into account the effect of compounding. Compounding refers to the interest accumulated on the principal. When the frequency of compounding your investment or debt is more than once a year, the effect of compounding comes into play, and the effective annual rate will be higher than the nominal annual rate.

This actual annualized return rate is known as the effective annual rate or annualized compound rate and can be calculated by the formula:

$$
\text{Effective Annual Rate (EAR)} = \left(1 + \frac{r}{n}\right)^{nt} – 1
$$

• EAR is the effective annual rate.
• r is the nominal annual rate.
• n is the number of compounding periods per year.
• t is the number of years.

When calculating the effective annual rate, t is usually taken as 1.

The Relationship Between the Effective Annual Rate and the Nominal Annual Rate

Due to the effect of compounding, in the case of multiple compounding periods within a year, the actual annualized return rate (or cost) will be higher than the nominal annual rate.

Nominal Annual Interest Rate	Compounding Periods per Year	Effective Annual Rate
2%	4	2.01%
3%	4	3.03%
4%	4	4.06%
5%	4	5.09%
6%	4	6.14%

Present Value

Definition

In finance, Present Value (PV) refers to the value of a future cash flow in today’s terms.

i.e. Present Value is the current value of a future sum of money, reflecting the impact of interest, inflation, risk, etc., on this future cash flow

Discount Rate

Definition

To calculate the present value, people usually use a discount rate (also known as the interest rate) to adjust future cash flows.

Types

The discount rate could be fixed or variable, depending on many factors, including the type of investment, the economic environment, expected changes in interest rates, risk levels, etc.

1. Fixed Discount Rate: When the investment has a fixed return rate, and significant economic changes are unlikely during the investment period, the discount rate is usually fixed. For example, when you purchase a fixed deposit or a government bond, these usually have a fixed interest rate, so the discount rate is also fixed.

2. Variable Discount Rate: In many cases, the discount rate will change with time and market conditions. For instance, investments with higher risk usually have a higher discount rate. Moreover, if the market expects interest rates to rise, the discount rate for future cash flows might also increase. Therefore, in riskier investments such as stock investment or real estate investment, the discount rate is usually variable.

Influencing Factors

The factors that may influence the discount rate include:

1. Expected Changes in Interest Rates: If the market expects interest rates to rise in the future, the discount rate may also increase.

2. Risk Level: Investments with higher risk usually require higher returns, so the discount rate would also be higher.

3. Economic Environment: If the economic outlook is uncertain or inflation expectations are rising, the discount rate may also increase.

4. Characteristics of the Investment: For example, the term of the investment, liquidity, credit rating, etc., all could impact the discount rate.

5. Investor’s Risk Preference: Different investors may have different risk tolerance and expected returns, which would also influence their chosen discount rate.

Characteristics

The higher the discount rate, the greater the uncertainty investors have about the future, or the greater their demand for money now. They prefer to have money now.

i.e. When the discount rate increases, the value of future cash flows as seen today (i.e., the present value) will decrease. This is because investors need a higher return to compensate for the greater risk they bear or the opportunity they give up to use the money now.

Simple Interest

The Present Value (PV) formula can be derived from the Future Value (FV) formula

$$
PV = \frac{FV}{(1 + r)^t}
$$

where:

• FV is the future value
• r is the annual interest rate
• t is the number of years – it doesn’t need to be an integer

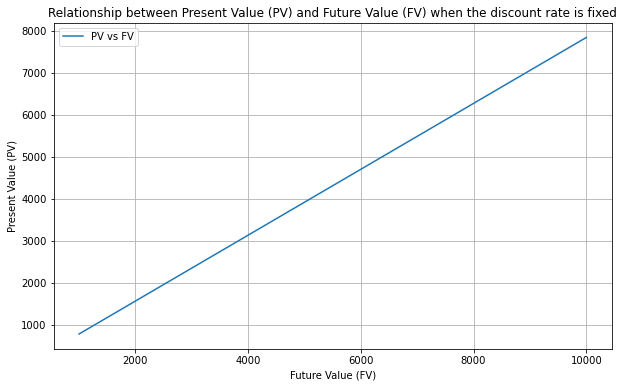
For example, if the future value in 5 years is 15000, and the annual interest rate is 5%, we can calculate the present value as follows:

FV = 15000 # Future Value
r = 0.05 # Annual Interest Rate
t = 5 # Number of Years

PV = FV / (1 + r)^t = 15000 / (1 + 0.05)^5 = 15000 / 1.27628 = 11748.68

Compound Interest

The Present Value (PV) formula can be derived from the Future Value (FV) formula

$$
PV = \frac{FV}{(1 + \frac{r}{n})^{nt}}
$$

where:

• FV is the future value
• r is the annual interest rate
• n is the number of compounding periods per year
• t is the number of years – it doesn’t need to be an integer

For example, if the future value in 5 years is 15000, and the annual interest rate is 5%, with 4 compounding periods per year (quarterly

Net PV

Definition

Net present value is the result of subtracting the present value of an investment’s costs from its present value of income.

NPV is an important tool that reflects the economic benefits of an investment project, taking into account the value of time and risk factors. However, its accuracy is highly dependent on the accurate prediction of cash flows and the reasonable setting of the discount rate.

Characteristics

If the NPV of an investment is positive, then the investment is profitable.
If the NPV of an investment is negative, then the investment is not profitable.

Formula

The basic calculation formula for NPV: discount all future periods’ cash flows to the present at a specific discount rate, and then subtract the initial investment. The formula is as follows:

$$
NPV = \sum \frac{CF_t}{{(1 + r)}^t} – \text{Initial Investment}
$$

The meaning of this formula is: For each future period’s cash flow CFt, we need to calculate its present value according to the discount rate r and time t, and add up the present values of all periods. Finally, we need to subtract the initial investment Initial_Investment from this total present value, and the result is the NPV.

Derivation

When we need to evaluate the profitability of an investment project, we cannot simply add up the future cash flows, but need to discount them to the present, i.e., calculate their present value. The discount rate r is a parameter that reflects the time value of money and includes factors such as inflation rate, investment risk, etc.

Discount formula:

$$
PV = \frac{CF}{{(1 + r)}^n}
$$

Finally, we need to add up the present values of all periods’ cash flows for the investment project, and then subtract the initial investment, and we get the NPV, which reflects the net gain of the investment project.

Net PV vs PV

	PV (Present Value)	NPV (Net Present Value)
Definition	PV is the present value of a single future cash flow	NPV is the total present value of a series of cash flows minus the initial investment
Calculation	PV = CF / (1 + r)^n	NPV = ∑ [CFt / (1 + r)^t] – Initial_Investment
Usage	PV is generally used to evaluate the value of a single cash flow or an investment	NPV is generally used to evaluate the total value of an investment project or multiple cash flows
Interpretation	The higher the PV, the higher the present value of the future single cash flow	The higher the NPV, the better the economic benefit of the investment project. If the NPV is positive, the project is profitable; if the NPV is negative, the project is loss-making
Assumption	The calculation of PV assumes that the future cash flow and the discount rate are certain	The calculation of NPV assumes that the future cash flow, discount rate, and initial investment are certain
Attention	PV does not directly consider the initial investment	NPV subtracts the initial investment during calculation, so it is net income