Pricing of a Straight Bond
Summary
Straight Bond
- pays regular interest payments
- returns the principal amount (also known as the face value or par value) to the bondholder at maturity.
Pricing Factors of a straight bond
- Bond cash flows
- Required yield
- Time value of money
Bond Cash Flows
The cash flows from a bond consist of two parts:
- Regular coupon payments
- The bond’s par value paid at maturity
The return an investor expects is the sum of these two cash flows.
Par Value
The par value of a bond, also known as face value or nominal value.
Definition: The amount a bond investor receives from the bond issuer at maturity.
Can it change: This is a fixed amount agreed by the investor at the time of purchasing the bond, the par value does not change with changes in market interest rates, it can’t change.
Amount: Typically \$1,000, although other amounts exist as well.
Example:
A bond with a face value of 1,000 – Regardless of how much you actually paid to buy the bond (i.e., the bond’s market price may be above, below, or equal to the face value), you will receive the 1,000 face value when the bond matures.
Annuity (Coupon Interest)
Definition: Regular interest payments received over the life of a bond are known as coupon payments or simply "coupons".
Frequency: It varies, but these interest payments are usually made twice a year, i.e., semiannually.
Calculation: The annual interest rate of a bond (also known as the coupon rate) is calculated based on the bond’s face value (not the price you actually paid).
Point of Confusion: Even if the market price of a bond is above or below its face value, the coupon interest paid is still based on the bond’s face value. Therefore, your actual rate of return (also known as yield) may be higher or lower than the bond’s annual interest rate, depending on the price you actually paid for the bond.
Example:
Payment Frequency: Semiannual
Annual Interest Rate: 9%
Face Value = 1000
Semiannual Coupon Interest = 1000 * 4.5% = 45
Cash Flow Diagram
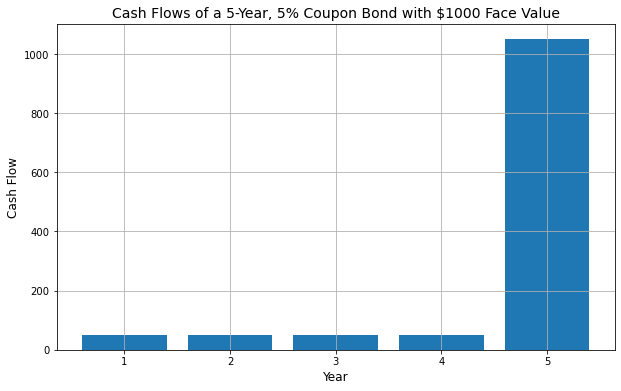
Impact of Annuity and Maturity Value on Bond Price
The bond price is roughly equal to the sum of future cash flows (including each period’s coupon payments and the principal repayment at maturity) discounted to the present.
Relationship:
- As the bond’s face value (or maturity value) increases, the amount discounted back increases, and the bond’s price increases.
- As the bond’s annuity (or coupon interest) increases, the amount discounted back increases, and the bond’s price increases.
Risk and Return Trade-Off
Q: Is it better to have a higher maturity value and annuity?
A: Not necessarily, because higher coupon payments or higher maturity values usually mean higher risks. The bond’s interest rate is a result reflecting the bond issuer’s debt repayment ability and various factors such as market interest rates. Therefore, the bond’s price, coupon rate, and maturity value are all factors that investors need to consider comprehensively.
- Credit Risk: Bond issuers might offer higher coupon payments to attract investors to purchase their bonds, especially when their credit rating is not high or there are problems with their ability to repay debts.
- Interest Rate Risk: There is an inverse relationship between interest rates and bond prices. When market interest rates rise, the price of existing bonds will fall, as newly issued bonds will offer higher rates. Therefore, high-coupon bonds may experience larger price fluctuations when interest rates rise, increasing the investment risk.
- Reinvestment Risk: If market interest rates decrease, investors might need to reinvest these received coupons at a lower interest rate. Therefore, high-coupon bonds may face higher reinvestment risks when interest rates fall.
Required Yield
Definition
The required yield is the minimum rate of return that an investor expects to obtain from a bond investment.
Influencing Factors
This is usually based on:
- The investor’s risk tolerance;
- Market conditions / market interest rates: as market interest rates increase, the rate of return that investors expect increases, as they have more investment opportunities to choose from;
- Other investment choices with a similar risk level;
- The credit risk of the bond: for bonds with lower credit ratings issued by the bond issuer, investors may require a higher required yield to compensate for possible credit risks;
- Economic conditions: if the economic outlook is uncertain, investors may require a higher required yield to compensate for risks.
Influence on Buying Bonds
When investors consider buying bonds, they will compare the bond’s coupon rate and their required yield:
- If the bond’s coupon rate > required yield, they may consider buying this bond;
- If the bond’s coupon rate < required yield, they may consider not buying this bond.
Relationship between Required Yield and Price at a Given Moment
Note: For bonds, the coupon rate and duration are fixed, so as market yield changes, the only thing that can compensate for the new yield is the bond’s price.
Inverse Relationship
- When the required yield increases, the bond price decreases;
- When the required yield decreases, the bond price increases.
Counterintuitive point: People might think that a higher yield (i.e., higher interest) would increase the attractiveness of the bond, thereby increasing its price. However, when we talk about bond yields, we are usually discussing market interest rates, or the return that investors can get from other investments with similar risks.
When market interest rates rise, although the bond’s regular interest payments do not change, the bond’s price must fall to increase the bond’s overall yield and keep it in line with the market interest rate.
Simple Explanation:
The interest payments of fixed-rate bonds become relatively unattractive after market interest rates rise, so
investors will demand a higher return (i.e., a lower price) to purchase such bonds.
Mathematical Proof:
As the yield increases, the rate of discounting future cash flows increases, the present value of future cash flows decreases, and the price drops.
Example:
If you have a 3% term deposit product and then a new 4% product appears on the market, the value of your original product in the market will fall because people can find products with higher returns in the market. The same principle applies to the bond market.
Convexity
(There will be a chapter specifically about convexity in the future)
If we draw the price/yield relationship, we will find it is bow-shaped.
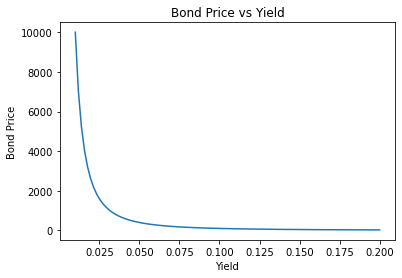
Reasons:
- Negative Correlation – There is a negative correlation between bond prices and interest rates.
- Non-linear – The negative correlation between bond prices and interest rates is non-linear. Convexity means that when yield changes, the change in bond prices is asymmetrical – when yield rises, bond prices fall, but the decrease is less than the increase in bond prices when yield falls. This non-linear relationship is due to the fixed future dates at which the bond’s future cash flows (i.e., interest payments and principal repayments) occur, and the impact of changes in these cash flows’ discount rate (i.e., yield) on bond prices becomes greater over time.
Function:
This convexity feature makes bonds have certain price stability when facing interest rate fluctuations, which is why investors pay attention to bond convexity when managing interest rate risk.
Long-term Bonds
Long-term bond prices are more sensitive to changes in the required yield. That is, all other things being equal, a small change in the required yield can lead to a significant fluctuation in the price of long-term bonds.
Pricing
Formula Derivation
The value of a bond is the sum of the present values (PV) of its future cash flows:
- The present value of future coupon payments
- The present value of future face value payments
The formula can be expressed as:
$$
\begin{aligned}
& \frac{c}{(1+i)}+\frac{c}{(1+i)^2}+\ldots+\frac{c}{(1+i)^n} \
\end{aligned}
$$
$$
\begin{aligned}
= & \sum_{t=1}^n \frac{c}{(1+i)^t} \
\end{aligned}
$$
$$
\begin{aligned}
= & c \cdot \frac{1-\frac{1}{(1+i)^n}}{i}
\end{aligned}
$$
Where:
$P=$ Price
$c=$ Semiannual coupon payment
$i=$ Periodic interest rate (required yield/2) (in decimal form)
$n=$ Number of periods (number of years × 2)
$M=$ Maturity value.
Example:
Suppose the required yield is 12%, calculate the price of a 20-year bond with a coupon rate of 9% and a face value of \$1000. This bond has the following cash flows:
- 40 semiannual coupon payments of \$45
- A maturity payment of \$1000 after 40 semiannual periods.
The semiannual interest rate (i.e., the periodic interest rate) is 6%. Discounting at 6%, the present value of 40 semiannual coupon payments of 45 is 677.08, as shown below:
$c=$ \$45
$n=$ 40
$i=$ 0.06
$$
\begin{array}{rl}
\$ & 45\left[\frac{1-\left[\frac{1}{(1.06)^{40}}\right]}{0.06}\right] \
& =\$45\left[\frac{1-\left[\frac{1}{10.28572}\right]}{0.06}\right] \
& =\$45(15.04630) \
\end{array}
$$
$$
\begin{array}{rl}
& =\$677.08
\end{array}
$$
Discounting at 6%, the present value of the \$1000 maturity payment after 40 semiannual periods is \$97.22, as shown below:
$M=$ \$1000
$n=$ 40
$i=$ 0.06
$$
\begin{aligned}
\$1000 \times \left(\frac{1}{(1.06)^{40}}\right) &= \$1000 \times \left(\frac{1}{10.28572}\right) \
\end{aligned}
$$
$$
\begin{aligned}
&= \$1000 \times (0.097222) \
&= \$97.22
\end{aligned}
$$
Therefore, the bond price is the sum of these two present values:
Present value of coupon payments + present value of maturity payment = bond price
$$
\begin{aligned}
\$677.08 + \$97.22 = \$774.30
\end{aligned}
$$
Discount, Coupon Rate & Price Relationship
The relationship between the bond’s discount rate and the bond’s
coupon rate is based on the bond’s pricing mechanism.
-
Bond Discount: If the market interest rate (or also called the required yield or discount rate) is higher than the bond’s coupon rate, then the bond will be sold at a discount. The reason is that investors are not willing to pay the full price for this bond because they can find higher yields in the market. Therefore, the bond price must be reduced (i.e., discounted) so that the overall yield of the bond matches the market interest rate. In this case, the bond price will be lower than its face value.
-
Bond Premium: Conversely, if the market interest rate is lower than the bond’s coupon rate, then the bond will be sold at a premium. This is because the return provided by the bond is higher than the market interest rate, and investors are willing to pay a higher price for it. In this case, the bond price will be higher than its face value.
-
Par Value Sale: If the market interest rate equals the bond’s coupon rate, then the bond will be sold at its face value.
Example:
Suppose a bond has a face value of \$1000 and a coupon rate of 5%, and it pays a coupon of \$50 per year. If the market interest rate (discount rate) is 6%, investors can get a 6% return elsewhere, so they will not be willing to pay the face value of \$1000 for a bond that only yields 5%. They will look for a discount so that the total yield of this bond reaches 6%. So, the price of this bond will be less than \$1000, i.e., the bond will be sold at a discount.
Conversely, if the market interest rate is 4%, the bond’s coupon rate of 5% is relatively high, and investors will be willing to pay more than the face value for this bond because it offers a return that exceeds the market. So, the price of this bond will be more than \$1000, i.e., the bond will be sold at a premium.
Finally, if the market interest rate is exactly 5%, the price of this bond will equal its face value of \$1000, as its yield matches the market yield.
Time Path of Bond Prices
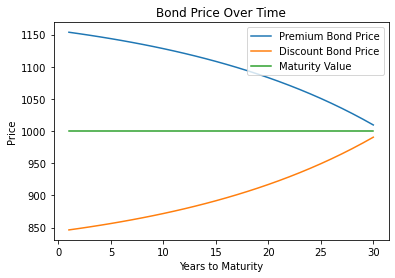
Reversion to Par Value
This phenomenon can be understood from the bond pricing formula. Essentially, the value of a bond is composed of two parts: the sum of the present values of its future cash flows (coupon income and face value at maturity). As time passes, the remaining term of the bond shortens, and the discounted values of these future cash flows get closer to their face values.
Eventually, on the maturity date, the value of the bond will equal its face value, because by then, the investor will receive a cash payment equal to the face value.
In Layman’s Terms
This makes sense because when investors purchase a bond, what they expect to receive is the face value of the bond at maturity and the coupon payments during the period. When the bond matures, the investors will receive the face value of the bond. So, as the maturity date approaches, investors are less likely to be willing to pay a price for the bond that is significantly higher or lower than the face value.
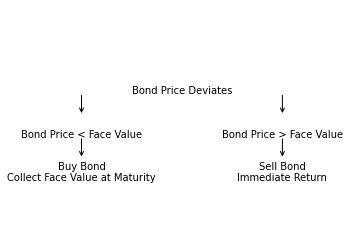
Arbitrage
Arbitrage opportunities arise if the bond price deviates significantly from its face value. For example, if a bond is close to maturity and its market price is significantly lower than its face value, investors can purchase the bond and then collect the face value at maturity, thereby achieving a return above the market price.
Conversely, if a bond is close to maturity but its market price is significantly higher than its face value, the bondholder can sell the bond in the market rather than waiting for it to mature.
For instance – suppose there is a bond with a face value of 1000, one year remaining to maturity, and an annual coupon income of 50, but it is priced at 900 in the market. This means that investors can purchase this bond for 900 and then receive a face value of 1000 and coupon income of 50 after one year, which is likely to be much higher than the return offered by other investment opportunities in the market. Similarly, if this bond is priced at 1100, the bondholder could opt to sell the bond in the market rather than waiting until maturity to receive only the 1000 face value.
Trading Quotes
Bonds are typically quoted as a percentage of their face value, a percentage often referred to as the "price."
For example, if a bond has a face value of 1000 and it is quoted at 105, this means that the price of the bond is 105% of 1000, or 1050.
This quotation method also applies to bonds sold at discount or premium prices. For instance, if a bond is quoted at 98, that means the bond’s price is 98% of 1000, or 980. This would be a discount bond, as its market price is lower than the face value.
Conversely, if a bond is quoted above 100, say 105, it is considered a premium bond because its market price is higher than its face value.
| Quote | Percentage of Face Value (\$1000) | Bond Price |
|---|---|---|
| 90 | 90% of \$1000 | \$900 |
| 95 | 95% of \$1000 | \$950 |
| 100 | 100% of \$1000 | \$1000 |
| 105 | 105% of \$1000 | \$1050 |
| 110 | 110% of \$1000 | \$1100 |