Methods of Equation Solving: Bisection and Newton’s Approach

Example Equation

Suppose we have the following cash flows:

• In the 0th year, we invest 100 units.
• In the 1st year, we receive 60 units.
• In the 2nd year, we receive 60 units.

We need to find an IRR that makes NPV equal to 0. That is, we need to find an IRR that satisfies the following equation:

$$
NPV = \frac{-100}{(1+IRR)^0} + \frac{60}{(1+IRR)^1} + \frac{60}{(1+IRR)^2} = 0
$$

Bisection Method

Definition

The bisection method is a very intuitive and simple way to find the root of an equation. The method is based on the Intermediate Value Theorem.

Conditions

1. Continuity: The target function needs to be continuous in the selected interval [a, b].

2. Existence: There must be at least one root in the given interval. In other words, for the interval endpoints a and b, the function values f(a) and f(b) need to have different signs. According to the Intermediate Value Theorem, if a continuous function has different signs at two points, then there is at least one root between these two points.

3. Uniqueness: Although this is not a strict requirement, if there are multiple roots in the given interval [a, b], then the bisection method can only find one of them. Therefore, ideally, there should only be one root in this interval.

Steps

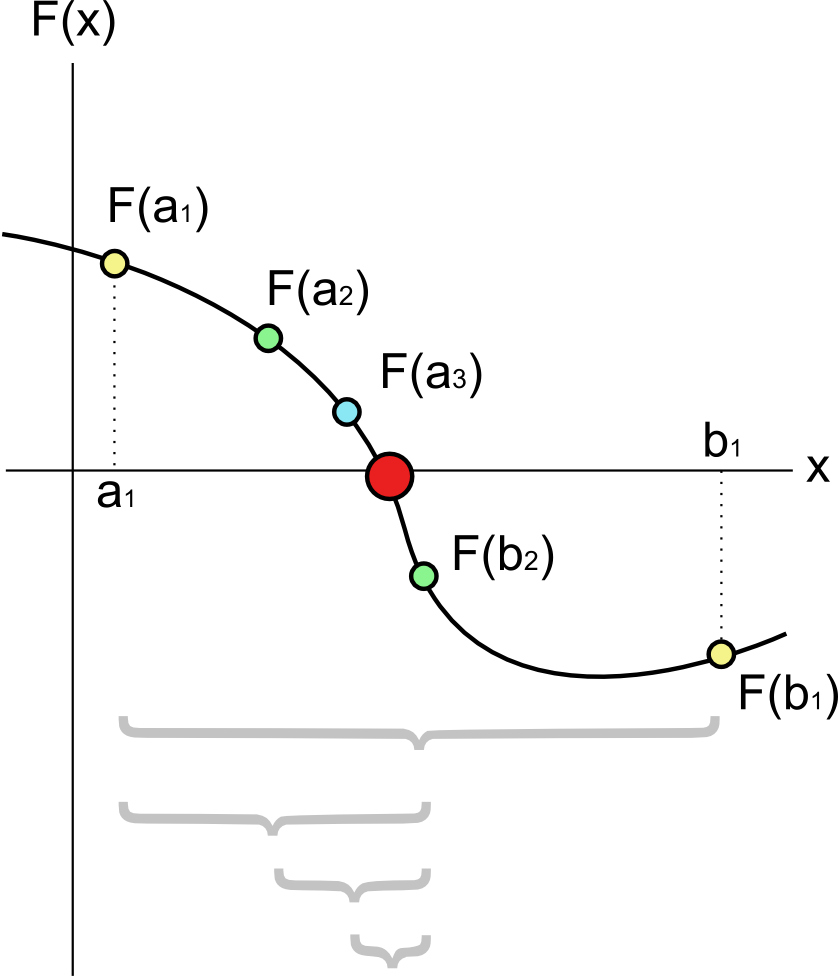
It assumes that the root of the equation is within an initial interval [a, b], and then narrows this interval by the following steps:

• Calculate the midpoint of the interval c = (a + b) / 2.
• If the sign of $f(c)$ is the same as that of $f(a)$, then the new interval is [c, b]; otherwise, the new interval is [a, c].
• Repeat the above steps until the length of the interval is less than a preset threshold.

Principle

The basic idea is to divide the search space of the problem into two parts, and judge which part the target value may be based on the properties of the problem

, and then further search in this part, continuously narrow the search space, until a solution that meets the conditions is found or a certain accuracy requirement is reached.

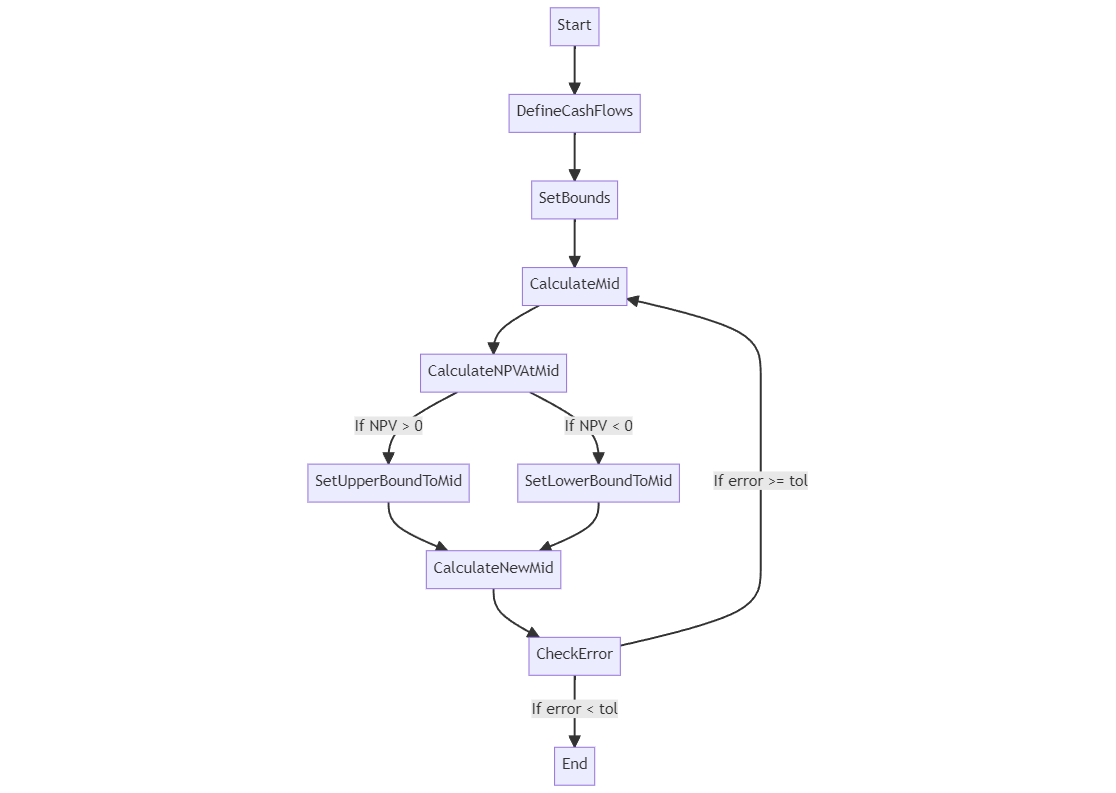
Flowchart

Example

1. Set the initial range of IRR, for example, 0 to 1.
2. Calculate the midpoint of the range, for example (0+1)/2 = 0.5.
3. Calculate the NPV value at the midpoint, i.e., NPV(0.5) = -100 + 60/(1+0.5) + 60/(1+0.5)^2 = -2.67 (this value is less than 0).
4. Because NPV(0.5)<0, we need to set the lower bound of IRR to 0.5. The new IRR range becomes 0.5 to 1.
5. Repeat steps 2 to 4 until the accuracy requirements are met.

Newton’s Method

Definition

Newton’s method is a method for approximating the solution of an equation in the real and complex number domains. The method uses the first few terms of the Taylor series of function f to find the root of the equation f(x)=0.

Conditions

1. Differentiability: The function must be differentiable on the interval of interest and preferably continuously differentiable. This is because Newton’s method requires the use of the first derivative of the function.

2. Initial Guess: Newton’s method is an iterative method that requires an initial guess. In the best case, this initial guess should be as close as possible to the actual root.

3. Existence: It needs to be ensured that the problem has at least one solution. Moreover, if there are multiple solutions, Newton’s method may only converge to one of them, depending on the initial guess.

4. Convergence: For certain special cases, Newton’s method may not converge. For example, when the initial guess is chosen at the point where the derivative of the function is zero, or in some cases, when the second derivative of the function changes drastically near the root, Newton’s method may not converge.

Steps

In each step, Newton’s method constructs the next guess by finding the root of the linear approximation of the function. This process can be described by the following formula:

$$
x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}
$$

In this formula, x_{n+1} is the new guess, x_n is the current guess, f(x_n) is the value of the function at x_n, and f'(x_n) is the derivative of the function at x_n.

Repeat this process, Newton’s method continuously updates the guess until it finds a solution that meets the accuracy requirements.

Calculate IRR:

Using Newton’s method, we need to

set an initial value, for example, 0.5. Then we need to calculate the NPV and its derivative at IRR, and use the following formula to update the value of IRR:

$$
IRR_{n+1} = IRR_n – \frac{NPV(IRR_n)}{NPV'(IRR_n)}
$$

where, $NPV'(IRR)$ is the derivative of NPV with respect to IRR, which can be calculated as:

$$
NPV'(IRR) = -\frac{0(-100)}{(1+IRR)^1} + \frac{-160}{(1+IRR)^2} + \frac{-2*60}{(1+IRR)^3}
$$

Repeat this process until you find an IRR that meets the accuracy requirements.

Principle

The key to Newton’s method is to use the local linear approximation of the function to approximate the root of the equation. Through continuous iteration, each time the intersection of the tangent at the approximate solution and the x-axis is chosen as the new approximate solution, gradually approaching the solution of the equation. When the derivative of the function is not zero near the solution and the initial guess solution is close enough to the real solution, Newton’s method can usually quickly converge to the solution of the equation.

Flowchart

Example

1. Set the initial IRR, for example, 0.5.
2. Calculate the NPV at the current IRR, i.e., NPV(0.5) = -100 + 60/(1+0.5) + 60/(1+0.5)^2 = -2.67.
3. Calculate the derivative of the NPV at the current IRR, i.e., NPV'(0.5) = -60/(1+0.5)^2 – 2*60/(1+0.5)^3 = 5.33.
4. Update the IRR value, i.e., IRR_new = 0.5 – NPV(0.5)/NPV'(0.5) = 0.5 – (-2.67/5.33) = 0.6.
5. Repeat steps 2 to 4 until the accuracy requirement is met.

Bisection Method vs Newton’s Method

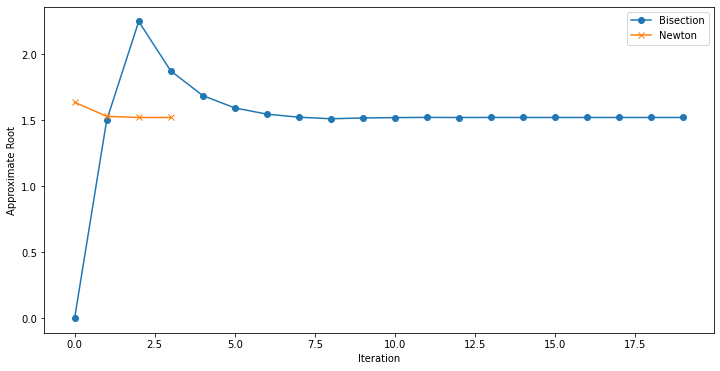
Convergence speed comparison chart

Item	Bisection Method	Newton’s Method
Speed	Slower. The convergence rate of the bisection method is linear, reducing about half the error at each step.	Faster. Under good conditions, the convergence rate of Newton’s method is quadratic, meaning it reduces the error square at each step.
Advantages	Simple and easy to implement. As long as a root exists and the required initial assumptions are met (the function has opposite signs at the interval endpoints), it can always find the root.	Under good conditions (like the function is continuous and differentiable near the root) and if the initial guess is close to the real root, Newton’s method converges faster than the bisection method.
Disadvantages	Convergence rate is slower. If there are multiple roots in a certain interval, specific choices may be required to find all roots.	Requires the derivative of the function. If the derivative of the function near the root is zero or changes dramatically, Newton’s method may not converge. Furthermore, the choice of initial guess is also important.
Conditions	The function is continuous on the given interval [a, b], and at the two ends of this interval, the function values have different signs.	The function is differentiable on the interested interval, and preferably continuously differentiable. A starting guess is required, preferably as close as possible to the actual root.
Limitations	It is necessary to know that the root is within a definite interval, which requires some prior knowledge of the problem. If there are multiple roots, more information or methods are needed to find all the roots.	Some functions may not have derivatives, or the derivatives at some points are zero, making it difficult to apply Newton’s method. Additionally, for complex functions, even if solutions exist, Newton’s method may not converge. The choice of initial guess can also affect convergence.