Trees
(Solutions can be found in my github repo )
A tree data structure can be defined recursively as a collection of nodes, where each node is a data structure consisting of a value and a list of references to nodes.
Trees should not have cycles
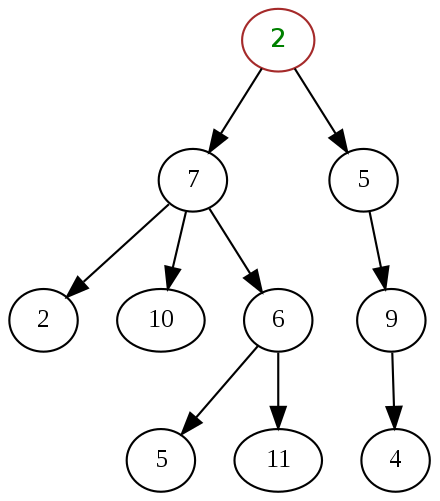
A straightforward class definition for Node:
class TreeNode(_value: Int = 0, _left: TreeNode = null, _right: TreeNode = null) {
var value: Int = _value
var left: TreeNode = _left // Leaf: left would be null
var right: TreeNode = _right // Leaf: right would be null
}Example tree
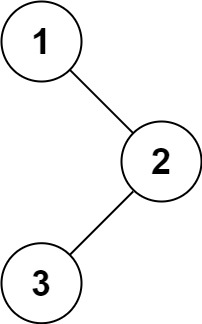
val three = TreeNode(3, null, null)
val two = TreeNode(2, three, null)
val one = TreeNode(1, null, two) // the root
Real World Examples
- Most XML/Markup parsers use trees. See Apache Xerces for example. Or, the Xalan XSLT parser.
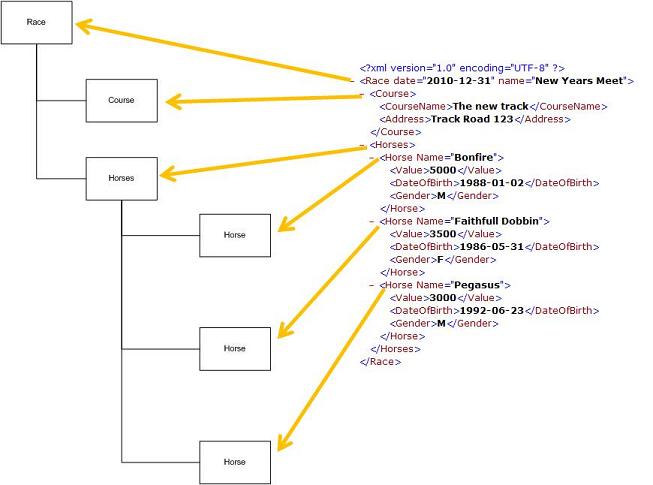
- PDF is a tree based format. It has a
rootnode followed by acatalognode(these are often the same) followed by apagesnode which has several childpagenodes. Producers/consumers often use a balanced tree implementation to store a document in memory.
-
Decision Tree based Learning actually forms a formidable area of data mining research. Numerous famous methods exist like bagging, boosting, and modifications thereof which work on trees. Such work is often used to generate a predictive model.
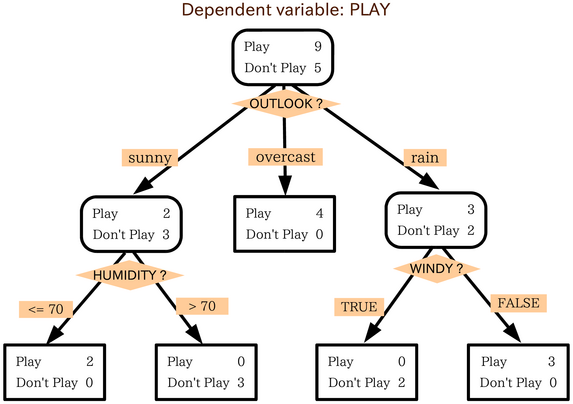
Terminology
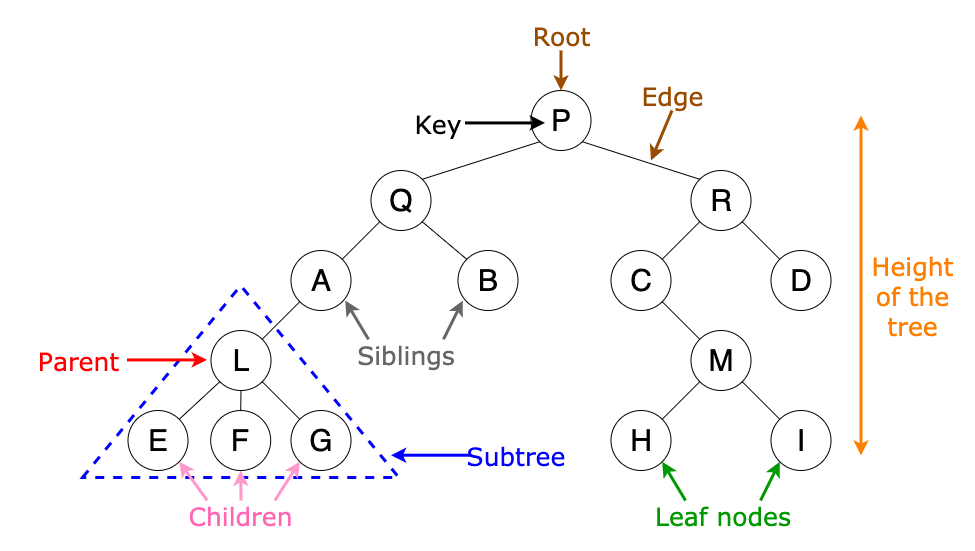
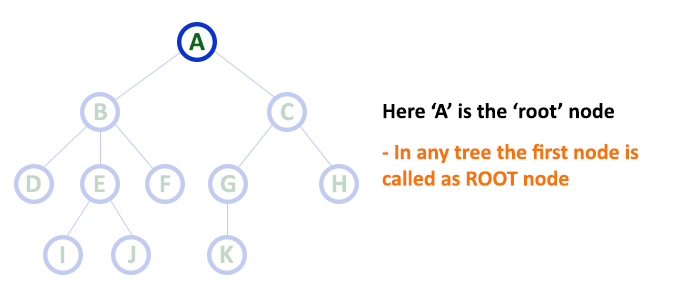
Root
The start of the tree is the "root node."
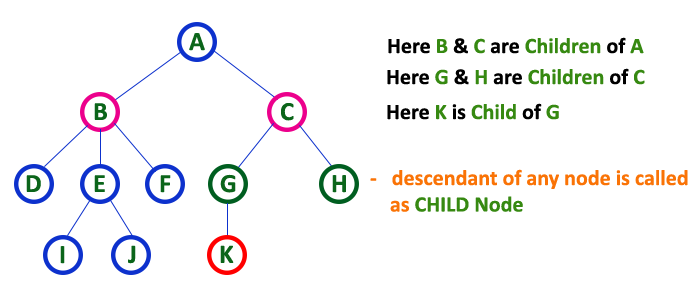
Children
Reference nodes are the "children."
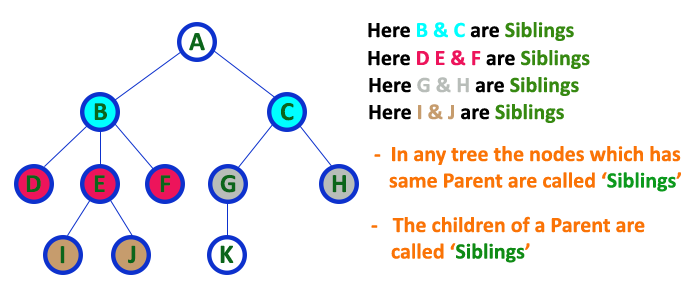
Siblings
In a tree data structure, nodes which belong to same Parent are called as SIBLINGS. In simple words, the nodes with the same parent are called Sibling nodes.
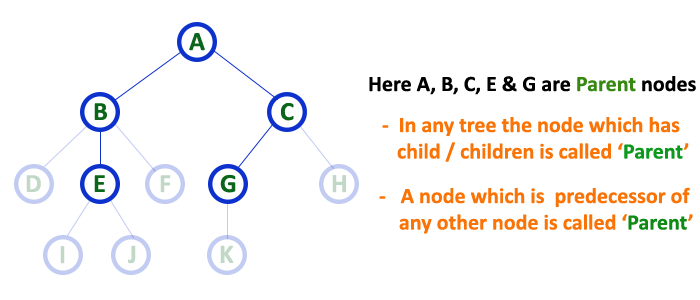
Parent
In a tree data structure, the node which is a predecessor of any node is called as PARENT NODE. In simple words, the node which has a branch from it to any other node is called a parent node. Parent node can also be defined as "The node which has child / children".
Neighbour
Parent or child.
Ancestor
A node is reachable by repeated proceeding from child to parent.
Descendant / Subchild
A node that is reachable by repeated proceeding from parent to child. Also known as sub child.
Internal Nodes
In a tree data structure, the node which has atleast one child is called as INTERNAL Node. In simple words, an internal node is a node with atleast one child.
In a tree data structure, nodes other than leaf nodes are called as Internal Nodes. The root node is also said to be Internal Node if the tree has more than one node. Internal nodes are also called as ‘Non-Terminal’ nodes.
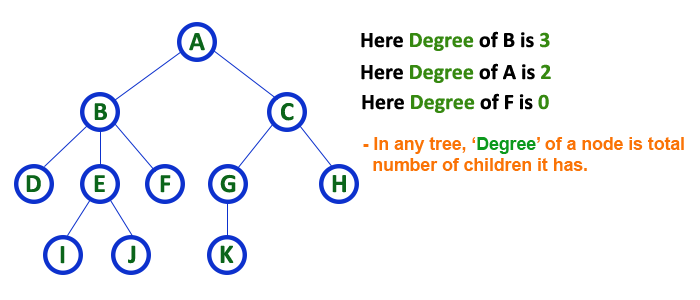
Degree
For a given node, its number of children. A leaf has necessarily degree zero.
Degree of Tree
The degree of a tree is the maximum degree of a node in the tree.
Depth
In a tree data structure, the total number of egdes from root node to a particular node is called as DEPTH of that Node. In a tree, the total number of edges from root node to a leaf node in the longest path is said to be Depth of the tree. In simple words, the highest depth of any leaf node in a tree is said to be depth of that tree. In a tree, depth of the root node is ‘0’.
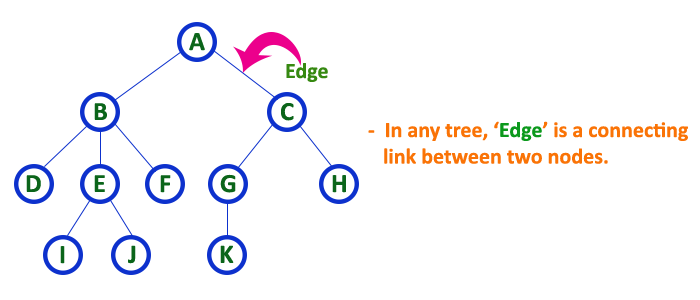
Edge
In a tree data structure, the connecting link between any two nodes is called as EDGE. In a tree with ‘N‘ number of nodes there will be a maximum of ‘N-1‘ number of edges.
Distance
"Distance" is the number of edges along the shortest path between two nodes.
Level
The level of a node is the number of edges along the unique path between it and the root node. In a tree data structure, the root node is said to be at Level 0 and the children of root node are at Level 1 and the children of the nodes which are at Level 1 will be at Level 2 and so on… In simple words, in a tree each step from top to bottom is called as a Level and the Level count starts with ‘0’ and incremented by one at each level (Step).
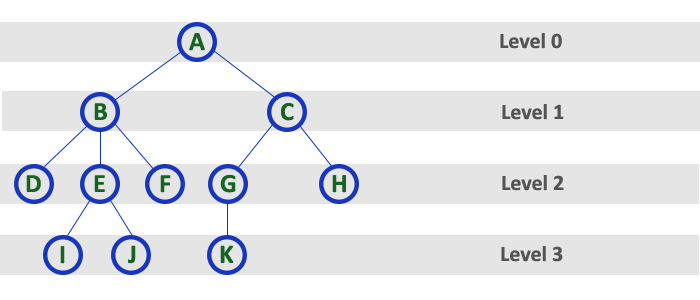
Width
The number of nodes in a level.
Height
In a tree data structure, the total number of edges from leaf node to a particular node in the longest path is called as HEIGHT of that Node. In a tree, height of the root node is said to be height of the tree. In a tree, height of all leaf nodes is ‘0’.
Breadth
The number of leaves.
Forest
A set of n ≥ 0 disjoint trees.
Sub Tree
In a tree data structure, each child from a node forms a subtree recursively. Every child node will form a subtree on its parent node.
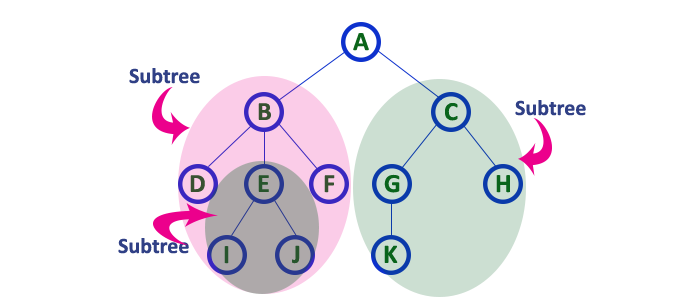
Size of a Tree
The number of nodes in the tree.
Leaf
A node is called a "leaf" if it has no children
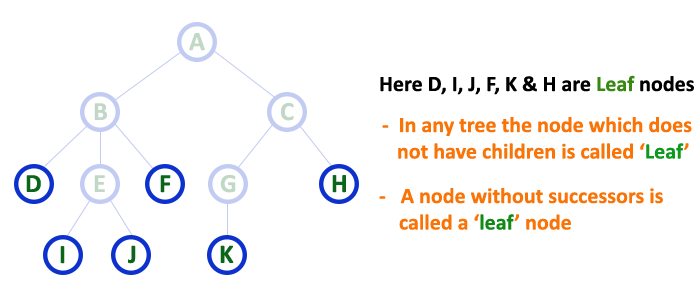
Different Types of Trees
Binary Tree
Each node has up to two children
Ternary Tree
Each node has up to three children
Binary Search Tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure whose internal nodes each store a key greater than all the keys in the node’s left subtree and less than those in its right subtree.
i.e. For a node with value n :
all left descendents <= n < all right descendents
Note: All descents – not just its immediate children
Not a binary search tree: 12 > 8
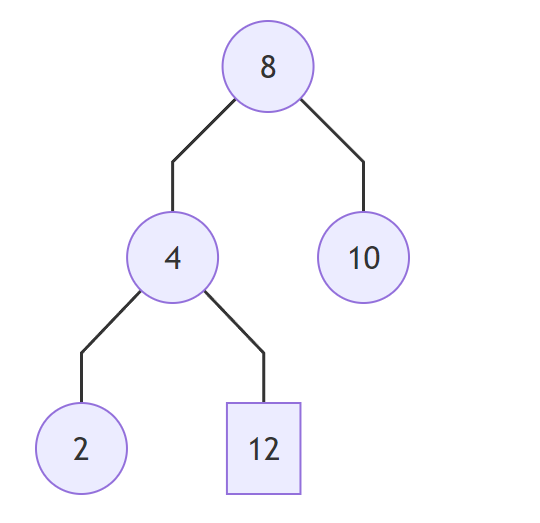
Figure: Binary search tree
Usage
A binary tree is a type of data structure for storing data such as numbers in an organized way. Binary search trees allow binary search for fast lookup, addition and removal of data items and can be used to implement dynamic sets and lookup tables.
Time Complexity
| Algorithm | Average | Worst case |
|---|---|---|
| Space | O( n ) | O( n ) |
| Search | O(log n) | O( n ) |
| Insert | O(log n) | O( n ) |
| Delete | O(log n) | O( n ) |
Validate Binary Search Tree
https://leetcode.com/problems/validate-binary-search-tree/
https://leetcode-cn.com/problems/validate-binary-search-tree/
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.
Example 1:

Input: root = [2,1,3]
Output: true
Example 2:

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node’s value is five, but its right child’s value is 4.
Solution
object LeetCode_98_Validate_Binary_Search_Tree {
def isValidBST(root: TreeNode): Boolean = {
validate(root, Long.MinValue, Long.MaxValue)
}
def validate(node: TreeNode, min: Long, max: Long): Boolean = {
if (node == null) true else {
if (node.value > min && node.value < max) {
validate(node.left, min, node.value) && validate(node.right, node.value, max)
} else false
}
}}
Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_98_Validate_Binary_Search_TreeTest extends AnyFunSuite with Matchers {
val tree1 = "2,1,3"
val tree2 = "5,1,4,null,null,3,6"
test("This tree is a valid BST") {
isValidBST(deserialize(tree1)) shouldBe true
}
test("This tree is not a valid BST") {
isValidBST(deserialize(tree2)) shouldBe false
}
}
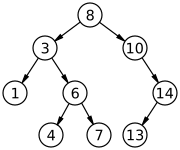
Balanced / Unbalanced
A tree that is balanced enough to ensure O(log n) times for search/insert/delete
Does not mean the left and right subtree are the same sizes – that is the "Perfect binary tree."
Figure: Balanced vs Unbalanced

Validation
https://leetcode-cn.com/problems/balanced-binary-tree/
https://leetcode.com/problems/balanced-binary-tree/
Given a binary tree, determine if it is height-balanced.
Example 1:
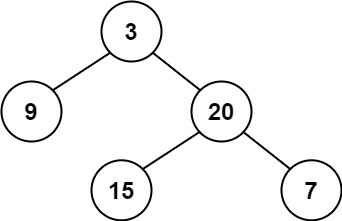
Input: root = [3,9,20,null,null,15,7]
Output: true
Example 2:
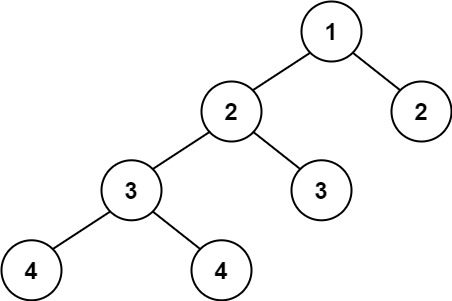
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false
Example 3:
Input: root = []
Output: true
Solution: For this problem, a height-balanced binary tree is defined as a binary tree in which every node’s left and right subtrees differ in height by no more than 1. Recursively check all nodes.
Solution
import scala.math._
object LeetCode_110_Balanced_Binary_Tree {
def getHeight(root: TreeNode): Int = {
if (root == null) 0 else {
max(getHeight(root.right), getHeight(root.left)) + 1
}
} def isBalanced(root: TreeNode): Boolean = {
if (root == null) true else {
val rootBalanced: Boolean = abs(getHeight(root.right) - getHeight(root.left)) <= 1
if (!rootBalanced) {
println(root)
} rootBalanced && isBalanced(root.left) && isBalanced(root.right)
} }}Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_110_Balanced_Binary_TreeTest extends AnyFunSuite with Matchers {
val tree1 = "4,-7,-3,null,null,-9,-3,9,-7,-4,null,6,null,-6,-6,null,null,0,6,5,null,9,null,null,-1,-4,null,null,null,-2"
val tree2 = "1,2,3,null,null,4,5"
test("tree1 is not a balanced tree") {
assert(isBalanced(deserialize(tree1)) == false)
}
test("tree2 is a balanced tree") {
isBalanced(deserialize(tree2)) shouldBe true
}
}Red-Black Trees
A red-black tree is a kind of self-balancing binary search tree. Each node stores an extra bit representing “colour” (“red” or “black”), used to ensure that the tree remains balanced during insertions and deletions.
When the tree is modified, the new tree is rearranged and “repainted” to restore the colouring properties that constrain how unbalanced the tree can become in the worst case. The properties are designed such that this rearranging and recolouring can be performed efficiently.

AVL Trees
An AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. It was the first such data structure to be invented. In an AVL tree, the heights of the two-child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

Complete Binary Tree
A complete binary tree is a binary tree in which all the levels are filled except possibly the lowest one, which is filled from the left.
Full Binary Tree
A full binary tree can be defined as a binary tree in which all the nodes have 0 or two children.
i.e. All the nodes have two children except the leaf nodes.

Perfect Binary Tree
- A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.
Provided the ancestry chart always displays the mother and the father on the same side for a given node, their sex can be seen as an analogy of left and right children, children being understood here as an algorithmic term. A perfect tree is therefore always complete, but a complete tree is not necessarily perfect.
Symmetric Tree
Symmetric: it is a mirror of itself (i.e., symmetric around its centre).
Validate Symmetric Trees
https://leetcode.com/problems/symmetric-tree/
https://leetcode-cn.com/problems/symmetric-tree/
Given the root of a binary tree, _check whether it is a mirror of itself
Example 1:
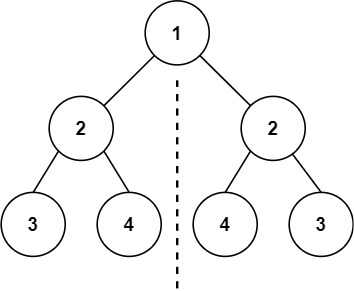
Input: root = [1,2,2,3,4,4,3]
Output: true
Example 2:
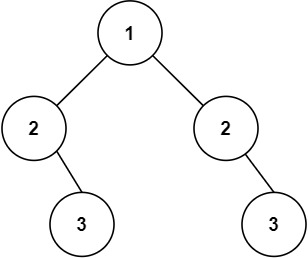
Input: root = [1,2,2,null,3,null,3]
Output: false
Solution: recursive check if the root’s left child and right child "mirror"
object LeetCode_101_Symmetric_Tree {
def isSymmetric(root: TreeNode): Boolean = {
if (root == null) true else {
isMirror(root.left, root.right)
} }
def isMirror(left: TreeNode, right: TreeNode): Boolean = {
if (left != null & right != null) {
left.value == right.value && isMirror(left.left, right.right) && isMirror(left.right, right.left)
} else if (left == null && right == null) true else false
}
}Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_101_Symmetric_TreeTest extends AnyFunSuite with Matchers {
val tree1 = deserialize("2,1,1")
val tree2 = deserialize("2,1,3")
test("return true if a tree is symmetric") {
isSymmetric(tree1) shouldBe true
}
test("return false if a tree is not symmetric") {
isSymmetric(tree2) shouldBe false
}
}Binary Tree Order Traversal

The root is the Kth part visited.
| Kth | |
|---|---|
| Pre-Order | 1st |
| In-Order | 2nd |
| Post-Order | 3rd |
: ) Now let us try this tree
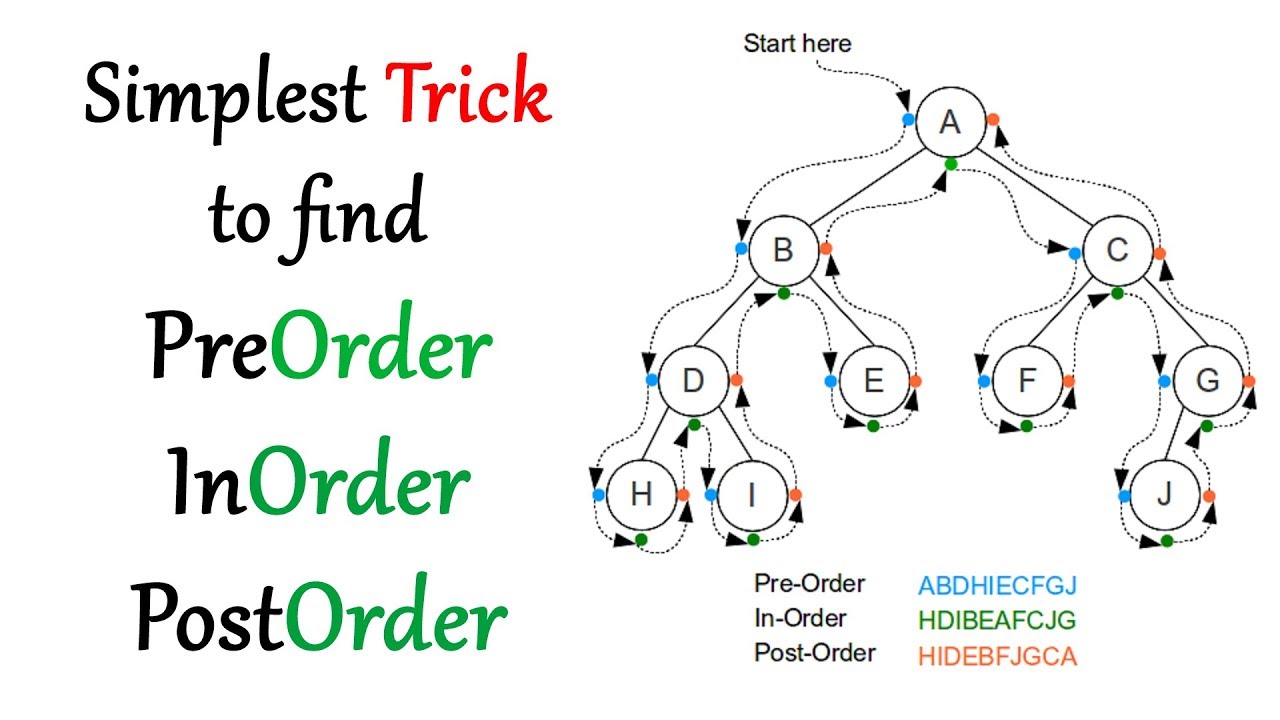
In-Order Traversal
Left branch -> Current node -> Right branch

When performed on a binary search tree, it visits the nodes in ascending order (i.e. in order)
https://leetcode.com/problems/binary-tree-inorder-traversal/
https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
Given the root of a binary tree, return the inorder traversal of its nodes’ values.
Example 1:

Input: root = [1,null,2,3]
Output: [1,3,2]
Solution
object LeetCode_94_Binary_Tree_Inorder_Traversal {
def inorderTraversal(root: TreeNode): List[Int] = {
if (root != null) {
{ inorderTraversal(root.left) :+ root.value
} ++ inorderTraversal(root.right)
} else List()
}}Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_94_Binary_Tree_Inorder_TraversalTest extends AnyFunSuite with Matchers {
test("Inorder traversal result of this tree should be List(1, 3, 2)") {
inorderTraversal(deserialize("1,null,2,3")) shouldBe List(1, 3, 2)
}}Pre-Order Traversal
Visits the current node before its child nodes
Current node -> Left branch -> Right branch

The root is always the first node visited.
https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
https://leetcode.com/problems/binary-tree-preorder-traversal/
Given the root of a binary tree, return the preorder traversal of its nodes’ values.
Example 1:

Input: root = [1,null,2,3]
Output: [1,2,3]
Solution
object LeetCode_144_Binary_Tree_Preorder_Traversal {
def preorderTraversal(node: TreeNode): List[Int] = {
if (node != null) {
node.value :: preorderTraversal(node.left) ++ preorderTraversal(node.right)
} else List()
}}Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_144_Binary_Tree_Preorder_TraversalTest extends AnyFunSuite with
Matchers {
test("Preorder traversal result of this tree should be List(1, 2, 3)") {
preorderTraversal(deserialize("1,null,2,3")) shouldBe List(1, 2, 3)
}}
Post-Order Traversal
Visits the current node after its child nodes
Left branch -> Right branch -> Current node

The root is always the last node visited.
https://leetcode.com/problems/binary-tree-postorder-traversal/
https://leetcode-cn.com/problems/binary-tree-postorder-traversal/
Given the root of a binary tree, return the postorder traversal of its nodes’ values.
Example 1:

Input: root = [1,null,2,3]
Output: [3,2,1]
Solution
object LeetCode_145_Binary_Tree_Postorder_Traversal {
def postOrderTraversal(node: TreeNode): List[Int] = {
if (node != null) {
postOrderTraversal(node.left) ++ postOrderTraversal(node.right) :+ node.value
// The root is always the last node visited.
} else List()
}}Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_145_Binary_Tree_Postorder_TraversalTest extends AnyFunSuite with
Matchers {
test("Preorder traversal result of this tree should be List(3, 2, 1)") {
postOrderTraversal(deserialize("1,null,2,3")) shouldBe List(3, 2, 1)
}}Level Order Traversal
Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
https://leetcode.com/problems/binary-tree-level-order-traversal/
Example:
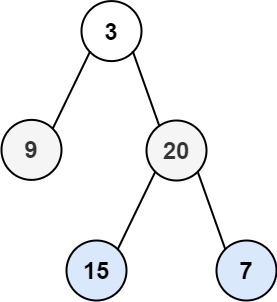
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]
Solution 1: Functional programming (immutable)
Well, I am a Scala person
import scala.annotation.tailrec
object LeetCode_102_Binary_Tree_Level_Order_Traversal {
def levelOrder(root: LeetCodeCN.TreeNode): List[List[Int]] = {
val currentTraversalResult = List()
if (root != null) {
traversal(List(root), currentTraversalResult)
} else currentTraversalResult
}
@tailrec
def traversal(currentLevel: List[LeetCodeCN.TreeNode], currentTraversalResult: List[List[Int]]): List[List[Int]] = {
if (currentLevel.nonEmpty) {
val newTraversalResult = currentTraversalResult :+ currentLevel.map(_.value)
val nextLevel: List[LeetCodeCN.TreeNode] = currentLevel.map(node => List(node.left, node.right)).flatten.filter(_ != null)
traversal(nextLevel, newTraversalResult)
} else currentTraversalResult
}
}Solution 2: Use Queue and ListBuffer (mutable)
import scala.collection.mutable
import scala.collection.mutable.ListBuffer
object LeetCode_102_Binary_Tree_Level_Order_Traversal {
def levelOrder(root: TreeNode): List[List[Int]] = {
if (root == null) return List[List[Int]]()
val result = new ListBuffer[List[Int]]()
val queue = new mutable.Queue[TreeNode]()
queue.enqueue(root)
while (queue.nonEmpty) {
val levelResult = new ListBuffer[Int]()
var levelSize = queue.size
while (levelSize > 0) {
val item = queue.dequeue()
levelResult.append(item.value)
if (item.left != null) {
queue.enqueue(item.left)
} if (item.right != null) {
queue.enqueue(item.right)
} levelSize = levelSize - 1
}
result.append(levelResult.toList)
} result.toList
}
}Test
import org.scalatest.funsuite.AnyFunSuite
import org.scalatest.matchers.should._
class LeetCode_102_Binary_Tree_Level_Order_TraversalTest extends AnyFunSuite with
Matchers {
test("Level order traversal result of this tree should be [[3],[9,20],[15,7]]") {
levelOrder(deserialize("3,9,20,null,null,15,7")) shouldBe List(List(3), List(9,
20), List(15, 7))
}}Serialize and Deserialize Trees
Serialization is converting a data structure or object into a sequence of bits to be stored in a file or memory buffer or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Construct String from Binary Tree
https://leetcode-cn.com/problems/construct-string-from-binary-tree/
Example 1:
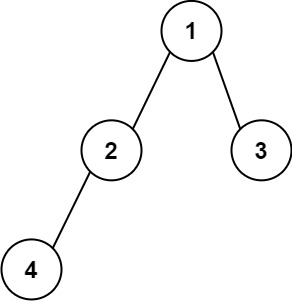
Input: root = [1,2,3,4]
Output: "1(2(4))(3)"
Explanation: Originally, it needs to be "1(2(4)())(3()())", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3)"
val four = TreeNode(4, null, null)
val three = TreeNode(3, null, null)
val two = TreeNode(2, four, null)
val one = TreeNode(1, two, three)
val emptyStr = ""
val emptyNode = "()"
def tree2str(root: TreeNode): String = {
if (root == null) emptyStr else {
val left = root.left
val right = root.right
val (leftStr, rightStr) = (left, right) match{
case (null, null) => (emptyStr,emptyStr)
case (left, null) => (s"(${tree2str(root.left)})", emptyStr)
case (null, right) => (emptyNode, s"(${tree2str(root.right)})")
case (left, right) => (s"(${tree2str(root.left)})", s"(${tree2str(root.right)})")
}
s"${root.value}" + leftStr + rightStr
}
}
println(tree2str(one))Find Duplicate Subtrees
https://leetcode.com/problems/find-duplicate-subtrees/
https://leetcode-cn.com/problems/find-duplicate-subtrees/
Given the root of a binary tree, return all duplicate subtrees.
For each kind of duplicate subtrees, you only need to return the root node of any one of them.
Two trees are duplicate if they have the same structure with the same node values.
Example 1:

Input: root = [1,2,3,4,null,2,4,null,null,4]
Output: [[2,4],[4]]
Example 2:

Input: root = [2,1,1]
Output: [[1]]
Example 3:

Input: root = [2,2,2,3,null,3,null]
Output: [[2,3],[3]]
val rightOne = TreeNode(1, null, null)
val leftOne = TreeNode(1, null, null)
val two = TreeNode(2, leftOne, rightOne)
val emptyNode = "()"
var dic: Map[String, (TreeNode, Int)] = Map()
// [2,1,11,11,null,1]
def tree2str(root: TreeNode): String = {
if (root == null) emptyNode else {
s"${root.value}(${tree2str(root.left)}(${tree2str(root.right)}"
}
}
def updateNodeDictionary(root: TreeNode): Unit = {
if (root != null) {
val nodeId = tree2str(root)
val nodeCount = dic.get(nodeId)
val newNodeCount = if (nodeCount.nonEmpty) {
nodeCount.get._2 + 1
} else {
1
}
dic += nodeId -> (root, newNodeCount)
updateNodeDictionary(root.left)
updateNodeDictionary(root.right)
}
}
def findDuplicateSubtrees(root: TreeNode): List[TreeNode] = {
updateNodeDictionary(root)
val duplicatedNodes: List[TreeNode] = dic.toSeq.collect { case (nodeId, (node, count)) if (count > 1) => node }.toList
dic = Map()
duplicatedNodes
}
println(findDuplicateSubtrees(two).map(_.value))Subtree of Another Tree
https://leetcode.com/problems/subtree-of-another-tree/
Given the roots of two binary trees, root and sub root, return true if there is a subtree of root with the same structure and node values of sub root and false otherwise.
A subtree of a binary tree is a tree consisting of a node in the tree and all of this node’s descendants. The tree could also be considered as a subtree of itself.
Example 1:
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true
Example 2:
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false
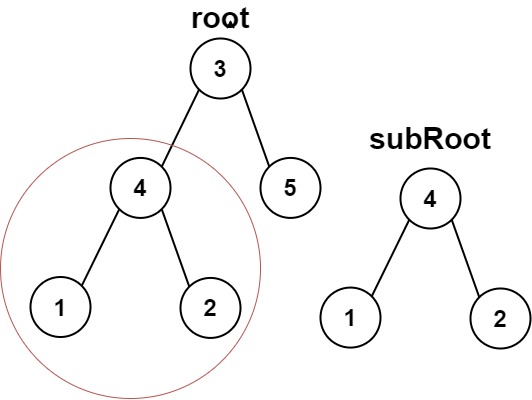
Example 2:
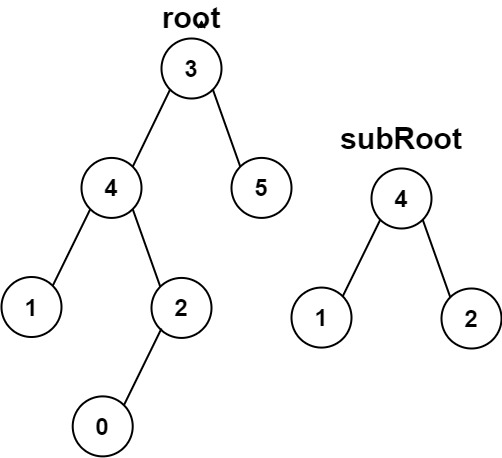
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false
Solution: Serialize all subtrees of the root, and store them in a set. Then, check if the subRoot is in the set.
val two = TreeNode(2, null, null)
val one = TreeNode(1, null, null)
val four = TreeNode(4, one, two)
val five = TreeNode(5, null, null)
val three = TreeNode(3, four, five)
val six = TreeNode(6, null, null)
val emptyNode = "()"
var subNodeSet: Set[String] = Set()
def tree2str(root: TreeNode): String = {
if (root == null) emptyNode else {
s"${root.value}(${tree2str(root.left)}(${tree2str(root.right)}"
}
}
def updateSubTreeSet(root: TreeNode): Unit = {
if (root != null) {
val nodeId = tree2str(root)
subNodeSet += nodeId
updateSubTreeSet(root.left)
updateSubTreeSet(root.right)
}
}
def isSubtree(root: TreeNode, subRoot: TreeNode): Boolean = {
val serializedSubRoot = tree2str(subRoot)
updateSubTreeSet(root)
val isSubtree = subNodeSet.contains(serializedSubRoot)
subNodeSet = Set()
isSubtree
}
println(isSubtree(three, four)) // true
println(isSubtree(three, six)) // falseFind Depth / Diameter of Trees
Example Tree:
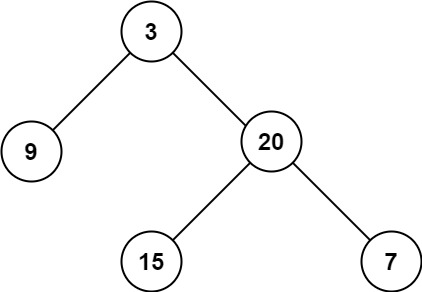
class TreeNode(_value: Int = 0, _left: TreeNode = null, _right: TreeNode = null) {
var value: Int = _value
var left: TreeNode = _left
var right: TreeNode = _right
}
val seventeen = TreeNode(17, null, null)
val fifteen = TreeNode(15, null, null)
val twenty = TreeNode(20, fifteen, seventeen)
val nine = TreeNode(9, null, null)
val root = TreeNode(3, nine, twenty)
Find Max Depth of Binary Tree
https://leetcode.com/problems/maximum-depth-of-binary-tree/
Given the root of a binary tree, return its maximum depth.
A binary tree’s maximum depth is the number of nodes along the longest path from the root node to the farthest leaf node.
Input: root = [3,9,20,null,null,15,7]
Output: 3
def maxDepth(root: TreeNode): Int = {
if (root == null) 0 else {
Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
}
}
println(maxDepth(root)) // 3Find Min Depth of Binary Tree
https://leetcode.com/problems/minimum-depth-of-binary-tree/

Use if-else
def minDepth(root: TreeNode): Int = {
if (root == null) 0 else {
if (root.left != null && root.right != null) {
Math.min(minDepth(root.left), minDepth(root.right)) + 1
} else if (root.left != null) {
minDepth(root.left) + 1
} else if (root.right != null) {
minDepth(root.right) + 1
} else 1
}
}
println(minDepth(root)) // 2Use matching
def minDepth(root: TreeNode): Int = {
if (root == null) 0 else {
val left = root.left
val right = root.right
(left, right) match {
case (null, null) => 1
case (null, right) => minDepth(right) + 1
case (left, null) => minDepth(left) + 1
case (left, right) => Math.min(minDepth(left), minDepth(right)) + 1
}
}
}
println(minDepth(root)) // 2Find diameter of Binary Tree
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The number of edges between them represents the length of a path between two nodes.
https://leetcode.com/problems/diameter-of-binary-tree/
Example 1:
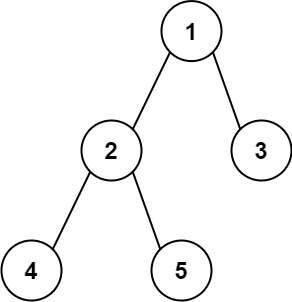
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
Solution
import scala.math.max
var diameters: Set[Int] = Set()
def maxDiameter(root: TreeNode): Int = {
if (root == null) 0 else {
val left = root.left
val right = root.right
(left, right) match {
case (null, null) => 1
case (left, null) => 1 + maxDiameter(left)
case (null, right) => 1 + maxDiameter(right)
case (left, right) => max(maxDiameter(right), maxDiameter(left)) + 1
}
}}
def addDiameterOfNode(root: TreeNode): Unit = {
val diameter = if (root == null) 0 else {
val left = root.left
val right = root.right
(left, right) match {
case (null, null) => 0
case (left, null) => maxDiameter(left)
case (null, right) => maxDiameter(right)
case (left, right) => maxDiameter(right) + maxDiameter(left)
} } diameters += diameter
}
def traversal(root: TreeNode): Unit = {
if (root != null) {
addDiameterOfNode(root)
addDiameterOfNode(root.left)
addDiameterOfNode(root.right)
}}
def diameterOfBinaryTree(root: TreeNode): Int = {
traversal(root)
val diameter = diameters.max
diameters = Set()
diameter
}Test
class LeetCode_543_Diameter_of_Binary_TreeTest extends AnyFunSuite {
val tree1 = "4,-7,-3,null,null,-9,-3,9,-7,-4,null,6,null,-6,-6,null,null,0,6,5,null,9,null,null,-1,-4,null,null,null,-2"
val tree2 = "1,2,3,null,null,4,5"
test("Return 3 for this tree's diameter") {
val tree = deserialize(tree2)
assert(diameterOfBinaryTree(tree) == 3)
}
test("Return 7 for this tree's diameter") {
val tree = deserialize(tree1)
assert(diameterOfBinaryTree(tree) == 7)
}}Relationships between Trees
Identical Trees
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
https://leetcode.com/problems/same-tree/
Example 1:
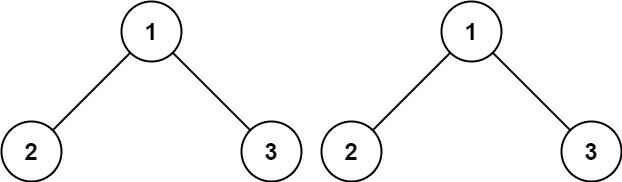
Input: p = [1,2,3], q = [1,2,3]
Output: true
Example 2:
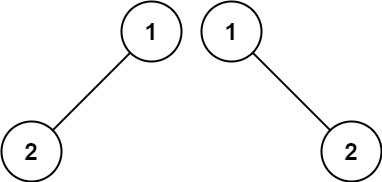
Input: p = [1,2], q = [1,null,2]
Output: false
Example 3:
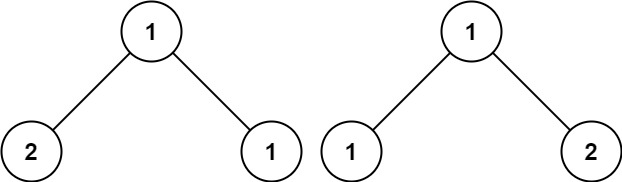
Input: p = [1,2,1], q = [1,1,2]
Output: false
Solution
The most straightforward strategy here is to use recursion. Check if p and q nodes are not "None", and their values are equal. If all checks are OK, do the same for the child nodes recursively.
def isSameTree(p: TreeNode, q: TreeNode): Boolean = {
(p, q) match {
case (null, null) => true
case (p, null) => false
case (null, q) => false
case (p, q) => {
p.value == q.value && isSameTree(p.left, q.left) && isSameTree(p.right, q.right)
}
}
}
Test
import main.scala.LeetCodeCN.LeetCode_100_Same_Tree.isSameTree
import main.scala.LeetCodeCN.TreeNode
import org.scalatest.funsuite.AnyFunSuite
class LeetCode_100_Same_TreeTest extends AnyFunSuite {
val three = TreeNode(3, null, null)
val one = TreeNode(1, null, null)
val two = TreeNode(2, one, three)
test("return true if two trees are the same") {
assert(isSameTree(two, two) == true)
}
test("return false if two trees are not the same") {
assert(isSameTree(one, two) == false)
}}Process Trees
Merge Two Binary Trees
https://leetcode-cn.com/problems/merge-two-binary-trees/
https://leetcode.com/problems/merge-two-binary-trees/
Other Problem Solving
Path Sum
https://leetcode.com/problems/path-sum/
Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum. (A leaf is a node with no children.)
Example :
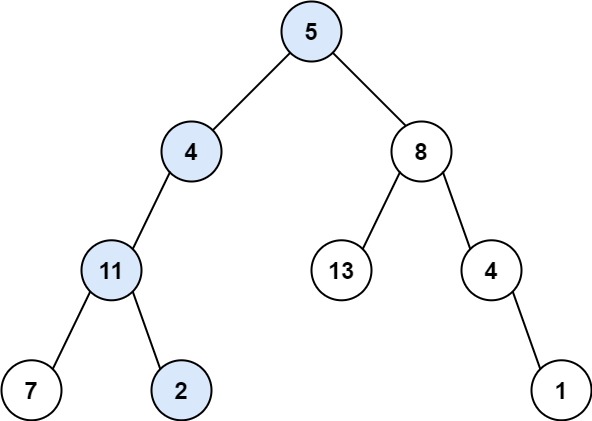
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
class TreeNode(_value: Int = 0, _left: TreeNode = null, _right: TreeNode = null) {
var value: Int = _value
var left: TreeNode = _left
var right: TreeNode = _right
}
// Build tree
val two = TreeNode(2, null, null)
val seven = TreeNode(7, null, null)
val eleven = TreeNode(11, seven, two)
val fourLeft = TreeNode(4, eleven, null)
val one = TreeNode(1, null, null)
val fourRight = TreeNode(4, null, one)
val thirteen = TreeNode(13, null, null)
val eight = TreeNode(8, thirteen, fourRight)
val root = TreeNode(5, fourLeft, eight)
def hasPathSum(root: TreeNode, targetSum: Int): Boolean = {
if (root == null) {
if (targetSum == 0) true else false
} else {
val left = root.left
val right = root.right
val rootValue = root.value
hasPathSum(left, targetSum - rootValue) || hasPathSum(right, targetSum - rootValue)
}
}
println(hasPathSum(root, 22)) // true
println(hasPathSum(root, 26)) // true
println(hasPathSum(root, 25)) // false Reference
- McDowell, G., n.d. Cracking the coding interview.
- En.wikipedia.org. 2021. Tree (data structure) – Wikipedia. [online] Available at: https://en.wikipedia.org/wiki/Tree_(data_structure) [Accessed 12 November 2021].
- En.wikipedia.org. 2021. Binary search tree – Wikipedia. [online] Available at: https://en.wikipedia.org/wiki/Binary_search_tree [Accessed 12 November 2021].
- Lcm.csa.iisc.ernet.in. 2021. 6.1.1 Implementation of Insert and Deletemin. [online] Available at: http://lcm.csa.iisc.ernet.in/dsa/node138.html [Accessed 14 November 2021].
- Medium. 2021. Binary Heap Basics. [online] Available at: https://medium.com/@verdi?p=40a0f3f41c8f [Accessed 14 November 2021].
- En.wikipedia.org. 2021. Trie – Wikipedia. [online] Available at: https://en.wikipedia.org/wiki/Trie [Accessed 14 November 2021].
- DroidTechKnow. 2021. An Introduction To Graph Data Structure. [online] Available at: https://droidtechknow.com/programming/data-structure/an-introduction-to-graph-data-structure/ [Accessed 14 November 2021].
- Leetcode-cn.com. 2021.. [online] Available at: https://leetcode-cn.com/ [Accessed 19 November 2021].
- Techie Me. 2021. Balanced Search Trees – AVL Tree – Techie Me. [online] Available at: http://techieme.in/balanced-search-trees-avl-tree/ [Accessed 24 November 2021].
- Programmercarl.com. 2021. _. [online] Available at: https://programmercarl.com/ [Accessed 28 November 2021].
- TechTalk7. 2021. Real world examples of tree structures – TechTalk7. [online] Available at: https://www.techtalk7.com/real-world-examples-of-tree-structures/ [Accessed 10 December 2021].
- Btechsmartclass.com. 2021. Data Structures Tutorials – Tree Terminology with examples. [online] Available at: http://www.btechsmartclass.com/data_structures/tree-terminology.html [Accessed 10 December 2021].