(7) Classes and Objects
About
:octocat: GitHub: All of the example code: repo (link)
:page_facing_up: blog link: https://purrgramming.life/cs/programming/fp/ :star:
Motivation of Using Data Structure
Here’s an example, say we want to design a package for doing rational arithmetic.
A rational number x/y is represented by two integers:
- its numerator x, and
- its denominator y
$$
\begin{aligned}
&\frac{3}{4}+\frac{4}{5} \
&=\frac{15}{20}+\frac{16}{20} \
&=\frac{31}{20}
\end{aligned}
$$
Example
$$
\begin{aligned}
&\frac{3}{5}+\frac{1}{4}=\frac{(12)}{(20)}+\frac{(5)}{(20)} \
&\frac{1}{3}-\frac{1}{24}=\frac{(8)}{(24)}-\frac{(1)}{(24)}
\end{aligned}
$$
Rational Number Rule 1/2:
\begin{aligned}
&\frac{n_{1}}{d_{1}}+\frac{n_{2}}{d_{2}}=\frac{n_{1} d_{2}+n_{2} d_{1}}{d_{1} d_{2}} \\
&\frac{n_{1}}{d_{1}}-\frac{n_{2}}{d_{2}}=\frac{n_{1} d_{2}-n_{2} d_{1}}{d_{1} d_{2}} \\
&\frac{n_{1}}{d_{1}} \cdot \frac{n_{2}}{d_{2}}=\frac{n_{1} n_{2}}{d_{1} d_{2}} \\
&\frac{n_{1}}{d_{1}} / \frac{n_{2}}{d_{2}}=\frac{n_{1} d_{2}}{d_{1} n_{2}} \\
&\frac{n_{1}}{d_{1}}=\frac{n_{2}}{d_{2}} \quad \text { if } \quad n_{1} d_{2}=d_{1} n_{2}
\end{aligned}Rational Number Rule 2/2:
Rational Simplify – We can reduce rational numbers to their smallest numerator and denominator by dividing both with a divisor.
$$
\begin{gathered}
\frac{6}{9}=\frac{2}{3} \
\
\frac{6 \div 3}{9 \div 3}=\frac{2}{3}
\end{gathered}
$$
Without Data structure
Rational Addition Suppose we want to implement the addition of two rational numbers.
def addRationalNumerator(n1: Int, d1: Int, n2: Int, d2: Int): Int
def addRationalDenominator(n1: Int, d1: Int, n2: Int, d2: Int): Int But it would be challenging to manage all these numerators and denominators.
With Data structure
A better choice is to combine the numerator and denominator of a rational number in a data structure.
Data Structures are a specialised means of organising and storing data in computers to perform operations on the stored data more efficiently.
Summary
As problems we solve become more complex, code design would be much harder.
Data structure provides abstracting, modelling, organising, managing, and efficiently storing data / solving problems.
i.e. Data structure provides efficiency, reusability and abstraction.
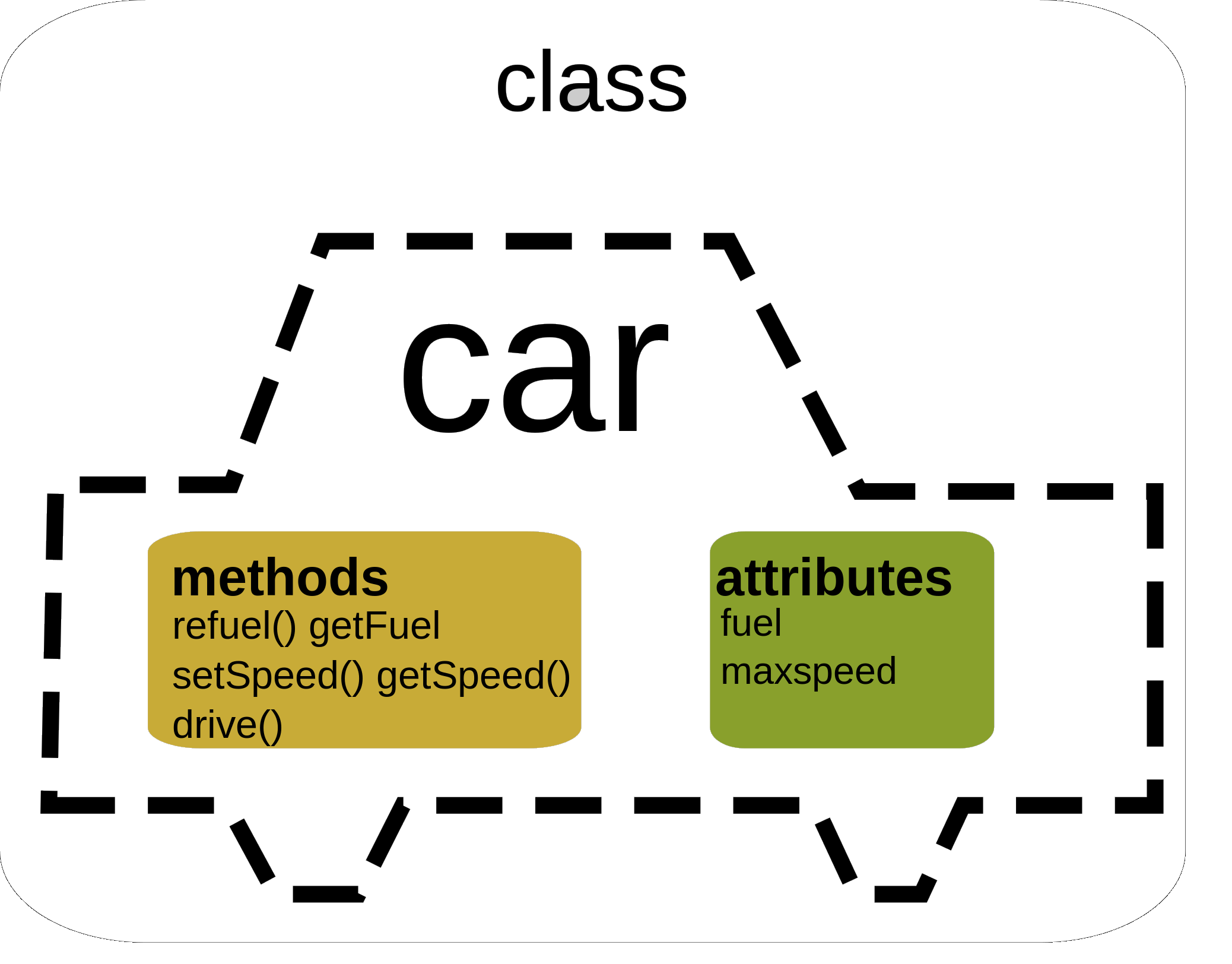
Classes
Definition
In object-oriented programming, a class is a template definition of the methods and variables in a particular kind of object.
image source: https://upload.wikimedia.org/wikipedia/commons/9/98/CPT-OOP-objects_and_classes_-_attmeth.svg
Constructor
In class-based object-oriented programming, a constructor is a special subroutine called to create an object.
It prepares the new object for use, often accepting arguments that the constructor uses to set required member variables.
Primary Constructors
In Scala, a class implicitly introduces a constructor. This one is called the primary constructor of the class.
The primary constructor
- takes the parameters of the class
- and executes all statements in the class body (requiring a couple of slides back).
Auxiliary Constructors
Scala also allows the declaration of auxiliary constructors. These are methods named this.
Example
Adding an auxiliary constructor to the class Rational for numbers whose denoms are 1.
def this(x: Int) = this(x, 1)Then we can run
val c = Rational(2)
// val c: Rational = 2/1Classes in Scala
In Scala, we do this by defining a class:
class Rational(x: Int, y: Int) {
def numer = x
def denom = y
}This definition introduces two entities:
- A new
type, namedRational. - A
constructorRational to create elements of this type. Scala keeps the names of types and values in different namespaces. So there’s no conflict between the two entities named Rational.
Self Reference
In computer programming, self-reference occurs in reflection.
A program can read or modify its own instructions like any other data.
The name this represents the object on which the current method is executed in a class.
def less(that: Rational): Boolean = {
(this.numer / this.denom) < (that.numer / that.denom)
}
// is the same as
def less2(that: Rational): Boolean = {
(numer / denom) < (that.numer / that.denom)
}
val x = Rational(1, 3)
val z = Rational(3, 2)
x less z // val res0: Boolean = true
x less2 z // val res1: Boolean = trueEnd Markers
With longer lists of definitions and deeper nesting, it’s sometimes harder to see where a class, function, or other construct ends.
End markers are a tool to make this explicit.
class Rational(x: Int, y: Int) {
...
}
end Rational - The end marker is followed by the name defined in the definition that ends at this point.
- It must align with the opening keyword (class in this case)
End markers are also allowed for other constructs.
When the end marker terminates a control expression such as if, the beginning keyword is repeated.
val x = 5
if (x == 3) println(s"it's $x")
else if (x == 4) println(s"it's $x")
else if (x == 5) println(s"it's $x")
else println(s"it's not 3, 4, or 5")
end if
// Result: it's 5
### Members and Methods
In object-oriented programming, a `member` variable (sometimes called a member field) is a variable that is associated with a specific object and accessible for all its methods (member functions).
i.e. An object consists of data and behaviour; these compose an interface, which specifies how various consumers may utilise the object.
The class `Rational` objects have two `members`, `numer` and `denom`.
We select the members of an object with the infix operator `.`
```scala
val x = Rational(1, 2)
x.numer // 1
x.denom // 2We can package functions operating on a data abstraction in the data abstraction itself – Such functions are called `methods`.
Members vs Methods
Member is a generic term that encompasses Constructors, Methods, and Fields.
A method is a function associated with an instance of a class or an object, i.e., a class's actions.
Objects
Singleton
In software engineering, the singleton pattern is a software design pattern that restricts the instantiation of a class to one "single" instance. This is useful when exactly one object is needed to coordinate actions across the system. The term comes from the mathematical concept of a singleton.
Official doc link
image source: https://obatambeienwasirherbal.com/php-design-pattern-singleton/imager_4_20653_700.jpg

In scala, an object is a class that has exactly one instance. It is created lazily when it is referenced, like a lazy val.
As a top-level value, an object is a singleton.
As a member of an enclosing class or as a local value, it behaves exactly like a lazy val.
Defining a Singleton Object
An object is a value. The definition of an object looks like a class but uses the keyword object:
object Box {
def info(message: String): Unit = println(s"INFO: $message of the box")
}Companion Object
Official doc: link
In Scala, a companion object is an `object` declared in the same file as a `class` and has the same name as the class.
Same Name
Q: Why they can use the same name?
A: An object and a class can have the same name. This is possible since Scala has two global namespaces: one for types and one for values. Classes live in the type namespace, whereas objects live in the namespace.
Benefits
Companion objects and their class can access each other’s private members (fields and methods) but is more flexible.
Example:
// Companion Object
// In the **same file** as Rational
object Rational {
def largerRationalNumber(thisRational: Rational, thatRational: Rational)
: Rational ={
if (thisRational less thatRational) thatRational else thisRational
}
}
import week2.lectureexample.Rational._
largerRationalNumber(c, d) // val res2: week2.lectureexample.Rational = 2/1
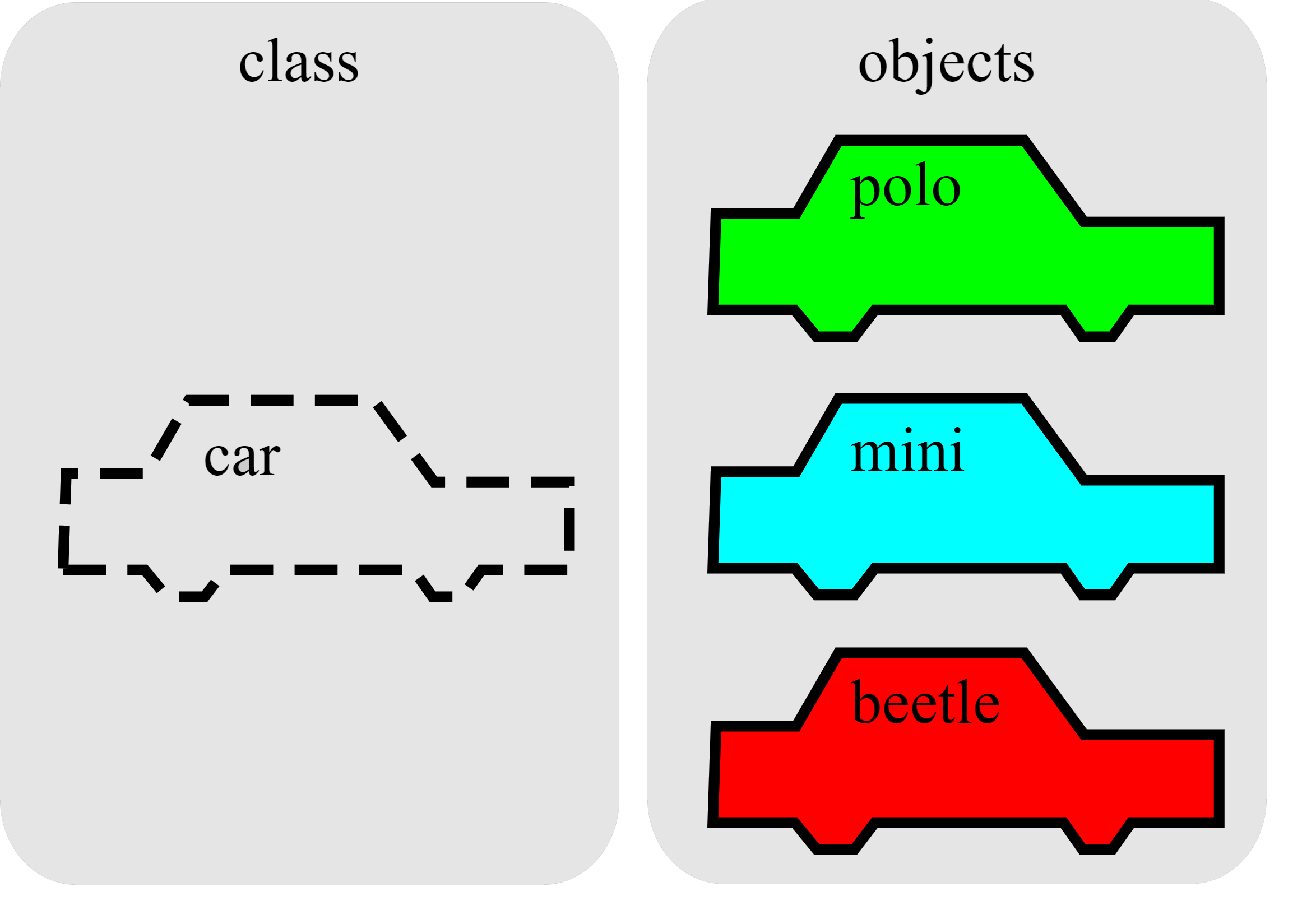
New Instance
When we create a new instance of a class
- It contains real values instead of variables
- We create an instance by calling the constructor of the class
like
Rational(1, 2)image source: https://commons.wikimedia.org/wiki/File:CPT-OOP-objects_and_classes.svg
Java static vs members in Scala Object
`static members` in Java are modelled as ordinary `members` of a `companion object` in Scala.
The members will be defined in a companion class with a static modifier when using a companion object from Java code. This is called static forwarding. It occurs even if you haven’t defined a companion class yourself.
Object vs Class
- A class is a blueprint of a particular classification of objects
- An object belongs to a class of objects
- A class can be created by using the ‘class’ keyword. An object can be created by using the ‘new’ keyword.
- An object is an instance of a class
- Memory space
- Class: not allocated
- Object: allocated
- Declaration
- Class: once
- Object: many times
When to use object
There is really only a single instance of it.
We can express this case better with an object definition.
Extension Methods
Defining all methods that belong to a class inside the class itself can lead to very large classes and is not very modular.
Methods that do not need to access the internals of a class can be defined as extension methods.
We can add abs method to class Rational like this:
extension (thisRational: Rational) {
def abs: Rational = Rational(thisRational.numer.abs, thisRational.denom)
}
val d = Rational(-2, 3)
d.abs // val res8: Rational = 2/3Note:
- Extensions can only add new members, not override existing ones.
- Extensions cannot refer to other class members via this
Extension method substitution works like normal substitution, but
- instead of `this`, it’s the extension parameter that gets substituted,
- class parameters are not visible, so they do not need to be substituted.
Summary
Extension methods
- cannot use 'this.'
- cannot override existing members
- cannot access private members of the class that they extend
- can define new members for a type
- can define infix operators
Operators
In principle, the rational numbers defined by Rational are as natural as integers. But for the user of these abstractions, there is a noticeable difference:
- We write `x + y` if x and y are integers, but
- We write ` r.add(s)` if `r` and `s` are rational numbers.
To eliminate this difference –
Step 1: Relaxed Identifiers
In programming languages, Identifiers are used for identification purposes. In Scala, an identifier can be a class, method, variable, or object name.
Operators such as `+` or `<` count as identifiers in Scala.
Thus, an identifier can be:
- Alphanumeric: starting with a letter, followed by a sequence of letters or numbers
- Symbolic: starting with an operator symbol, followed by other operator symbols.
- The underscore character ’_’ counts as a letter.
- Alphanumeric identifiers can also end in an underscore, followed by operator symbols.
Since operators are identifiers, it is possible to use them as method names.
def +(that: Rational): Rational = this.add(that)
def *(that: Rational): Rational = this.mul(that)
val a = Rational(2, 4)
val b = Rational(4, 2)
val c = Rational(2)
a * b // val res2: Rational = 1/1
c + c // val res7: Rational = 4/1
Step 2: Infix Notation
An operator method with a single parameter can be used as an infix operator.
An alphanumeric method with a single parameter can also be used as an infix operator if it is declared with an infix modifier.
infix def *(that: Rational): Rational = this.mul(that)
val a = Rational(2, 4)
val b = Rational(4, 2)
a.*(b) // val res2: Rational = 1/1
infix def min(that: Rational): Rational = {
if (this less that) this else that
}
x min z // val res2: week2.lectureexample.Rational = 1/3
r.min(s) // val res3: week2.lectureexample.Rational = 1/3Precedence Rules
The precedence of an operator is determined by its first character.
The following table lists the characters in increasing order of priority precedence:
(all letters)
|
^
&
< >
= !
:
+ -
* / %
(all other special characters)Homework – OOP Rational Numbers
Rational numbers now would have, in addition to the functions `numer` and `denom`, the functions `add, sub, mul, div, equal, toString`.
- In your worksheet, add a method neg to class Rational that is used like this:
x.neg // evaluates to -x - Add a method `sub` to subtract two rational numbers.
- With the values of `x, y, z` as given, what is the result of `x – y – z`
val x = Rational(1, 3)
val y = Rational(5, 7)
val z = Rational(3, 2)
Solution
import scala.annotation.tailrec
import scala.math.abs
class Rational(x: Int, y: Int) {
require(y != 0, "denominator cannot be 0")
def rationalGcd = {
gcd(x, y)
}
def equals(that: Rational): Boolean = {
this.numer == that.numer && this.denom == that.denom
}
def neg = {
Rational(-this.numer, denom)
}
def mul(that: Rational): Rational = {
Rational(this.numer * that.numer, this.denom * that.denom)
}
def div(that: Rational): Rational = {
val reciprocal = Rational(that.denom, that.numer)
this mul reciprocal
}
def add(that: Rational): Rational = {
Rational(
this.numer * that.denom + that.numer * this.denom,
this.denom * that.denom)
}
def less(that: Rational): Boolean = {
(this.numer / this.denom) < (that.numer / that.denom)
}
def less2(that: Rational): Boolean = {
(numer / denom) < (that.numer / that.denom)
}
def sub(that: Rational): Rational = {
this add that.neg
}
def numer = x / rationalGcd
def denom = y / rationalGcd
override def toString: String = s"${this.numer}/${this.denom}"
def this(x: Int) = this(x, 1)
def +(that: Rational): Rational = this.add(that)
infix def *(that: Rational): Rational = this.mul(that)
infix def min(that: Rational): Rational = {
if (this less that) this else that
}
// Greatest common divisor
@tailrec private def gcd(a: Int, b: Int): Int = {
if b == 0 then a else gcd(b, a % b)
}
}
end Rational
// Companion Object
object Rational {
def largerRationalNumber(thisRational: Rational, thatRational: Rational)
: Rational = {
if (thisRational less thatRational) thatRational else thisRational
}
}
import Rational.largerRationalNumber
val x = Rational(1, 3)
val y = Rational(5, 7)
val z = Rational(3, 2)
x less z // val res0: Boolean = true
x less2 z // val res1: Boolean = true
x min z // val res2: Rational = 1/3
// val illegal = Rational(4, 0) // IllegalArgumentException: denom cannot be 0
x.neg.toString // val res0: String = -1/3
x sub y sub z // val res1: Rational = -79/42
val a = Rational(2, 4)
val b = Rational(4, 2)
val c = Rational(2)
val d = Rational(-2, 3)
largerRationalNumber(c, d) // val res2: Rational = 2/1
a mul b // val res2: Rational = 1/1
a * b // val res2: Rational = 1/1
a.*(b) // val res2: Rational = 1/1
c + c // val res7: Rational = 4/1
a div a // val res3: Rational = 1/1
extension (thisRational: Rational) {
def abs: Rational = Rational(thisRational.numer.abs, thisRational.denom)
}
d.abs // val res8: Rational = 2/3
Rational(2, 4).toString // val res4: String = 1/2
Rational(2, 4) equals Rational(1, 2) // val res4: Boolean = true