(5) Higher-Order Functions
About
:octocat: GitHub: All of the example code: repo (link)
:page_facing_up: blog link: https://purrgramming.life/cs/programming/fp/ :star:
Topics
- Higher-Order Functions
- Currying
First-Class Values
A first-class object, first-class citizen, or first-class value is a language entity (e.g., function or variable) that operates as other entities in a language.
Functional languages treat functions as first-class values.
i.e. Like any other value, a function can be
- passed as a parameter
- returned as a result.
This provides a flexible way to compose programs.
Higher-Order Functions
Functions that take other functions as parameters or that return functions as results are called higher-order functions.
Normal Summing Functions:
//Take the sum of the integers between a and b:
def sumInts(a: Int, b: Int): Int =
if a > b then 0 else a + sumInts(a + 1, b)
//Take the sum of the cubes of all the integers between a and b :
def cube(x: Int): Int = x * x * x
def sumCubes(a: Int, b: Int): Int =
if a > b then 0 else cube(a) + sumCubes(a + 1, b)
def factorial(n: Int): Int =
if n == 0 then 1 else n * factorial(n - 1)
//Take the sum of the factorials of all the integers between a and b :
def sumFactorials(a: Int, b: Int): Int =
if a > b then 0 else factorial(a) + sumFactorials(a + 1, b)These are special cases of
$$
\sum_{n=a}^{b} f(n)
$$
for different values of f. Can we factor out the common pattern?
Summing with Higher-Order Functions
// Summing with Higher-Order Functions
// Let’s define:
def sum(f: Int => Int, a: Int, b: Int): Int =
if a > b then 0
else f(a) + sum(f, a + 1, b)
// when
def id(x: Int): Int = x
def cube(x: Int): Int = x * x * x
def fact(x: Int): Int = if x == 0 then 1 else x * fact(x - 1)
//We can then write:
def sumInts(a: Int, b: Int) = sum(id, a, b)
def sumCubes(a: Int, b: Int) = sum(cube, a, b)
def sumFactorials(a: Int, b: Int) = sum(fact, a, b)
sumInts(1, 2) // val res0: Int = 3
sumCubes(1, 2) // val res1: Int = 9
sumFactorials(1, 2) // val res2: Int = 3Function Types
The type A => B is the type of a function that takes an argument of type A and returns a result of type B.
So, Int => Int is the type of functions that map integers to integers.
Anonymous Functions / λ
An anonymous function is also called
- function literal
- λ lambda abstraction
- λ lambda function
- λ lambda expression / block
Definition
An anonymous function is
- not bound to an identifier
- is often an argument being passed to higher-order functions
- or used for constructing the result of a higher-order function that needs to return a function.
Motivation
Passing functions as parameters leads to the creation of many small functions.
So sometimes it is tedious to define (and name) these functions using def.
Compare to strings:
We do not need to define a string using def. Instead of
def str = ”abc”; println(str) We can directly write
println(”abc”) because strings exist as literals.
Motivations
- Analogously, we would like function literals, which let us write a function without giving it a name. These are called anonymous functions.
- If the function is only used once or a limited number of times, an anonymous function may be syntactically lighter than using a named function.
Anonymous Functions are Syntactic Sugar (syntax within a programming language designed to make things easier to read or express.)
Example
A function that raises its argument to a cube:
(x: Int) => x * x * x Here, (x: Int) is the parameter of the function, and x * x * x is it’s body.
The parameter type can be omitted if it can be inferred by the compiler from the context. If there are several parameters, they are separated by commas:
(x: Int, y: Int) => x + ySo sumInts and sumInts we wrote previously can be updated to
def sum(f: Int => Int, a: Int, b: Int): Int =
if a > b then 0
else f(a) + sum(f, a + 1, b)
def sumInts(a: Int, b: Int) = sum(x => x, a, b)
def sumCubes(a: Int, b: Int) = sum(x => x * x * x, a, b)
sumInts(1, 2) // val res0: Int = 3
sumCubes(1, 2) // val res1: Int = 9Exercise
The sum function uses linear recursion. Write a tail-recursive
def sum(f: Int => Int, a: Int, b: Int): Int =
if a > b then 0
else f(a) + sum(f, a + 1, b)
//----------------
// Lecture homework
//The sum function uses linear recursion.
//Write a tail-recursive version
def tailRecursiveSum(f: Int => Int, start: Int, end: Int): Int = {
@tailrec def loop(current: Int, acc: Int): Int =
if current == end then acc + f(current)
else loop(current + 1, acc + f(current))
loop(start, 0)
}
def tailRecursiveSumInts(a: Int, b: Int) = tailRecursiveSum(x => x, a, b)
def tailRecursiveSumCubes(a: Int, b: Int) = tailRecursiveSum(x => x * x * x, a, b)
tailRecursiveSumInts(1, 2) // val res0: Int = 3
tailRecursiveSumCubes(1, 2) // val res1: Int = 9Currying
About the Name
It’s not related to curry the food
It is named after logician Haskell Curry
Definition
In mathematics and computer science, currying is converting a function that takes multiple arguments into a sequence of functions that each takes a single argument.
image source: https://miro.medium.com/max/1152/1*OHN2sWFzuWY7gP_dqOQoeA.png
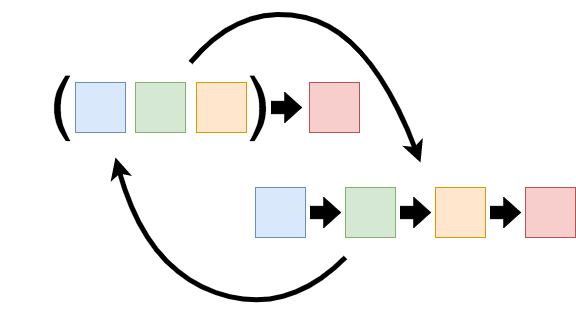
For example, currying a function f that takes three arguments creates three functions:
$$
\begin{gathered}
x=f(a, b, c) \text { becomes: } \
h=g(a) \
i=h(b) \
x=i(c)
\end{gathered}
$$
or called in sequence:
$$
x=g(a)(b)(c)
$$
Motivation
- Have to take only one argument
Currying provides a way to work with functions that take multiple arguments and use them in frameworks where functions might take only one argument.
For example, some analytical techniques can only be applied to functions with a single argument.
-
Support partial application
The programming technique of closures can be used to perform partial application and a kind of currying by hiding arguments in an environment that travels with the curried function. -
Enable supporting functions returning functions and stepwise applications
Example
Look again at the summation functions:
def sum(f: Int => Int, a: Int, b: Int): Int =
if a > b then 0
else f(a) + sum(f, a + 1, b)
def cube(x: Int): Int = x * x * x
def sumCubes(a: Int, b: Int) = sum(x => x * x * x, a, b)Q: Note that
aandbget passed unchanged from sumInts and sumCubes into sum.
Can we be even shorter by getting rid of these parameters?
Rewrite sum as follows to make it a function returning functions
def sumCurry(f: Int => Int): (Int, Int) => Int = {
def sumLoop(a: Int, b: Int): Int =
if a > b then 0
else f(a) + sumLoop(a + 1, b)
sumLoop
}We can then define some stepwise applications.
def sumCubesCurry = sumCurry(x => x * x * x) These functions can in turn be applied like any other function:
sumCubesCurry(1, 10) // val res1: Int = 3025This consecutive Stepwise Applications is the same as
sumCurry(cube)(1, 10) // val res1: Int = 3025Here, sum (cube) (1, 10)
sum(cube)applies sum to cube and returns the sum of cubes function.sum(cube)is therefore equivalent tosumCubes.- This function is next applied to the arguments
(1, 10).
Note: Function application associates to the lef
i.e.
sumCurry(cube)(1, 10) == (sumCurry (cube)) (1, 10)Multiple Parameter Lists
Finally, we can rewrite the cube function to
def cleanSum(f: Int => Int)(a: Int, b: Int): Int = {
if a > b then 0 else f(a) + cleanSum(f)(a + 1, b)
}where the type of #cleanSum is
(Int => Int) => (Int, Int) => IntHomework – Impl Map Reduce
- Write a
#productfunction that calculates the product of the values of a function for the points on a given interval. - Write factorial in terms of product.
- Can you write a more general function that generalizes both
sum
andproduct
// 1. Write a `#product` function that calculates the product of the
// values of a function for the points on a given interval.
def product(f: Int => Int)(a: Int, b: Int): Int = {
if a > b then 1 else f(a) * product(f)(a + 1, b)
}
// 1 * 2 * 3 = 6
product(x => x)(1, 3) // val res0: Int = 6
// 1 * 4 * 9 = 36
product(x => x * x)(1, 3) // val res0: Int = 36
// ----------------------------------------
// 2. Write factorial in terms of product.
// 2 * 3 * 4 * 5 = 120
def fact(n: Int) = product(x => x)(1, n)
fact(5) // val res2: Int = 120
// ----------------------------------------
// 3. Can you write a more general function which generalizes both sum
// and product
def mapReducedCalc(initial: Int)(operator: (Int, Int) => Int)(mapFunction: Int => Int)(start: Int, end: Int): Int
= {
if start > end then initial else operator(mapFunction(start),
mapReducedCalc(initial)(operator)(mapFunction)(start + 1, end))
}
// 1 + 2 + 3 = 6
mapReducedCalc(0)((x, y) => x + y)(x => x)(1, 3) // val res1: Int = 6
// 2 * 3 * 4 * 5 = 120
mapReducedCalc(1)((x, y) => x * y)(x => x)(1, 5) // val res4: Int = 120