(4) Recursion

About

:octocat: GitHub: All of the example code: repo (link)

:page_facing_up: blog link: https://purrgramming.life/cs/programming/fp/ :star:

---

Topics

1. Recursion
2. Tail Recursion
3. Coursework solutions

---

Background

Recursion is the process of defining a problem (or the solution to a problem) in terms of (a simpler version of) itself.
For example, we can define the operation "find your way home" as Stop moving if you are at home.

image source: https://stackoverflow.com/questions/13242050/java-recursion-triangle-with-deviation

Recursion

In Scala, recursive functions are functions that include calls to themselves in their definition, they

• do not always terminated
• require an explicit return type in Scala (the return type can be omitted in non-recursive functions, but it is required by the compiler for recursive functions)
• are not introduced by a dedicated keyword

Example: squareRoot

We will define in this session a function

/** Calculates the square root of parameter x */ 
def squareRoot(x: Double): Double = ... 

The classical way to achieve this is by successive approximations using Newton’s method.

To compute squareRoot(x):

• Start with an initial estimate y (let’s pick y = 1).
• Repeatedly improve the estimate by taking the mean of y and x/y.

image source: https://blogs.sas.com/content/iml/2016/05/18/newtons-method-babylonian-square-root.html

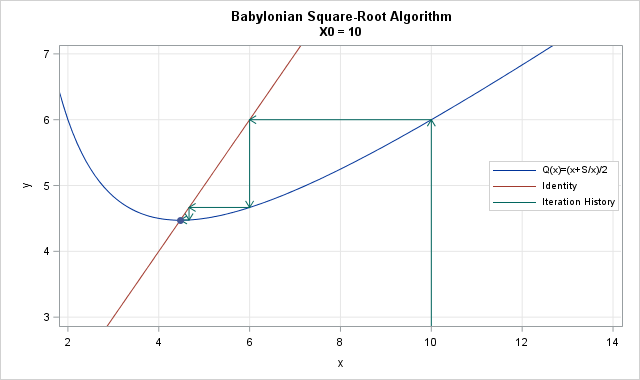
Example: x = 2

Estimation	Quotient	Mean
1	2 / 1=2	1.5
1.5	2 / 1.5=1.333	1.4167
1.4167	2 / 1.4167=1.4118	1.4142
1.4142	…	…

image source: https://demonstrations.wolfram.com/FindingATangentLineToAParabola/

So, let us

1. define a test to check for termination
2. define a function improve to improve an estimate
3. define a function that computes one iteration step
   • Note that squareRootIterator is recursive; its right-hand side calls itself.
4. define the squareRoot function

import scala.math.{abs, pow, sqrt}  

// define the squareRoot function:  
def squareRoot(squareNum: Double) = {  
  // define what is "Good enough"  
  // Avoid magic numbers 
  val accuracy = 0.001  

  // define a test to check for terminatation:  
  def isGoodEnough(guessedSquareRoot: Double) =  
    abs(guessedSquareRoot * guessedSquareRoot - squareNum) < accuracy  

  // define a function improve to improve an estimate  
  def improve(guessedSquareRoot: Double) =  
    (guessedSquareRoot + squareNum / guessedSquareRoot) / 2  

 // define a function which computes one iteration step  
 // Note that `squareRootIterator` is recursive, 
 // its right-hand side calls itself.  

def squareRootIterator(guessedSquareRoot: Double): Double =  
    if (isGoodEnough(guessedSquareRoot)) guessedSquareRoot  
    else squareRootIterator(improve(guessedSquareRoot))  

  squareRootIterator(1.0)  
}  

// Results are not bad  
squareRoot(4)  
// val res0: Double = 2.0000000929222947  
squareRoot(2)  
// val res1: Double = 1.4142156862745097

Limitation

Double not accurate: are infinite possible real numbers and an only finite number of bits to represent these numbers, so:

• The isGoodEnough test is not very precise for small numbers
• The isGoodEnough test is non-termination for very large numbers.

Bad Examples

• 0.001 – not very precise
• 10^(50) – non-termination

// Bad example
squareRoot(0.001)  
// val res2: Double = 0.04124542607499115  

// Correct answer  
sqrt(0.001) 
// val res3: Double = 0.03162277660168379  

// -------------------------

val largeNumber: Double = pow(10, 50)  

// Correct answer  
sqrt(largeNumber) 
// val res4: Double = 1.0E25  

// Bad example
squareRoot(largeNumber) 
// Never terminate 

Tail Recursion

Definition

If a function calls itself as its last action, like the greatest common divisor, the function’s stack frame can be reused with tail recursion.

In summary, a tail-recursive function

• are iterative processes
• can be optimized by reusing the stack frame in Scala
• calls itself as its last action

Tail Recursion Example

Example of tail recursion functions, i.e., A recursive function that calls itself as its last action

Impl of the function that computes the greatest common divisor of two numbers using Euclid’s algorithm:

Please note: it calls itself as its last action

// Euclid’s algorithm  
// Greatest Common Divisor
def gcd(a: Int, b: Int): Int = {  
  if b == 0 then a else gcd(b, a % b)  
}  

gcd(14, 21)// val res0: Int = 7  

//→ if 21 == 0 then 14 else gcd(21, 14 % 21)  
//→ if false then 14 else gcd(21, 14 % 21)  
//  → gcd(21, 14 % 21)  
//  → gcd(21, 14)  
//→ if 14 == 0 then 21 else gcd(14, 21 % 14)  
//  →→ gcd(14, 7)  
//  →→ gcd(7, 0)  
//→ if 0 == 0 then 7 else gcd(0, 7 % 0)  
//  → 7

Non-Tail Recursion Example

Example of non-tail recursion functions, i.e., A recursive function that does not calls itself as its last action.

Consider factorial:

def factorial(n: Int): Int =  
  if n == 0 then 1 else n * factorial(n - 1)  

factorial(4) // val res1: Int = 24  

//→ if 4 == 0 then 1 else 4 * factorial(4 - 1) 3-> →→ 4 * factorial(3)  
//  →→ 4 * (3 * factorial(2))  
//  →→ 4 * (3 * (2 * factorial(1)))  
//  →→ 4 * (3 * (2 * (1 * factorial(0)))  
//  →→ 4 * (3 * (2 * (1 * 1)))  
//  →→ 24

@tailrec

Tail recursion can be annotated with @tailrec so that the compiler will succeed only if it can verify that the function is indeed tail recursive, i.e. performance optimization.

import scala.annotation.tailrec  
@tailrec def gcd(a: Int, b: Int): Int = {  
  if b == 0 then a else gcd(b, a % b)  
}

Note: If we try to add `tailrec` to non tail recursive functions like `factorial`, we will get error

@tailrec \\ ERROR: Cannot rewrite recursive call: it is not in tail position  
def factorial(n: Int): Int =  
  if n == 0 then 1 else n * factorial(n - 1)

non @tailrec -> @tailrec

We can change non @tailrec recursive functions to @tailrec.

@tailrec def factorialTailRec(n: Int, lastFactorial: Int): Int =  
  if n == 0 then lastFactorial else factorialTailRec(n - 1, n * lastFactorial)  

factorialTailRec(4, 1) // val res1: Int = 24

W1 Coursework

Pascal's Triangle

The following pattern of numbers is called Pascal's triangle.

1  
1 1  
1 2 1  
1 3 3 1  
1 4 6 4 1  
...

The numbers at the edge of the triangle are all 1, and each number inside the triangle is the sum of the two numbers above it. Write a function that computes the elements of Pascal's triangle using a recursive process.

Do this exercise by implementing the pascal function, which takes a column c and a row r, counting from 0 and returns the number at that spot in the triangle. For example, `pascal(0,2)=1, pascal(1,2)=2 and pascal(1,3)=3.`

def pascal(col: Int, row: Int): Int = {  
  if (col == 0 && row == 0) 1 else if (col < 0 | row < 0) 0  
  else pascal(col - 1, row - 1) + pascal(col, row - 1)  
}

Testing

def main(args: Array[String]): Unit =  
  println("Pascal's Triangle")  
  for row <- 0 to 10 do  
 for col <- 0 to row do  
  print(s"${pascal(col, row)} ")  
    println()

Result

1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1 
1 6 15 20 15 6 1 
1 7 21 35 35 21 7 1 

Parentheses Balancing

Write a recursive function that verifies the balancing of parentheses in a string, which we represent as a List[Char], not a String. For example, the function should return true for the following strings:

• (if (zero? x) max (/ 1 x))

• I told him (that it's not (yet) done). (But he wasn't listening)

The function should return false for the following strings:

• : - )

• ())(

The last example shows that it's not enough to verify that a string contains the same number of opening and closing parentheses.

Do this exercise by implementing the balance function. Its signature is as follows:

def balance(chars: List[Char]): Boolean

There are three methods on List[Char] that are useful for this exercise:

• chars.isEmpty: Boolean returns whether a list is empty

• chars.head: Char returns the first element of the list

• chars.tail: List[Char] returns the list without the first element

Hint: you can define an inner function if you need to pass extra parameters to your function.

Testing: You can use the toList method to convert from a String to a List[Char]: e.g. `"(just an) example".toList.`

def balance(chars: List[Char]): Boolean = {  
  var parenthesesStack = new Stack[Char]()  

  @tailrec def balanceRec(chars: List[Char]): Boolean = {  
    if (parenthesesStack.isEmpty && chars.isEmpty) true  
 else if (parenthesesStack.nonEmpty && chars  
      .isEmpty) false else {  
      chars.last match {  
        case ')' => {  
          parenthesesStack.push(')')  
          balanceRec(chars.dropRight(1))  
        }  
        case '(' => {  
          if (parenthesesStack.nonEmpty && parenthesesStack.pop == ')') balanceRec(chars.dropRight(1))  
          else false  
  }  
        case _ => balanceRec(chars.dropRight  
        (1))  
      }  
    }  
  }  

  val isBalanced = balanceRec(chars)  
  parenthesesStack = Stack[Char]()  
  isBalanced  

}

Counting Change

Write a recursive function that counts how many different ways you can change an amount, given a list of coin denominations. For example, there are 3 ways to change for 4 if you have coins with denominations 1 and 2: 1+1+1+1, 1+1+2, 2+2.

Do this exercise by implementing the countChange function. This function takes an amount to change and a list of unique denominations for the coins. Its signature is as follows:

def countChange(money: Int, coins: List[Int]): Int

Once again, you can use functions isEmpty, head and tail on the list of integers coins.

Hint: Think of the degenerate cases. How many ways can you give change for 0 dollars? How many ways can you give change for >0 dollars if you have no coins?

def countChange(money: Int, coins: List[Int]): Int = {  
  if (money < 0 || coins.isEmpty) 0  
  else if (money == 0) 1  
  else {  
    val withFirstCoin = countChange(money - coins.head, coins)  
    val withoutFirstCoin = countChange(money, coins.drop(1))  
    withFirstCoin + withoutFirstCoin  
  }  
}