(1) Principles of Functional Programming

About

:octocat: GitHub: All of the example code: repo (link)

:page_facing_up: blog link: https://purrgramming.life/cs/programming/fp/ :star:

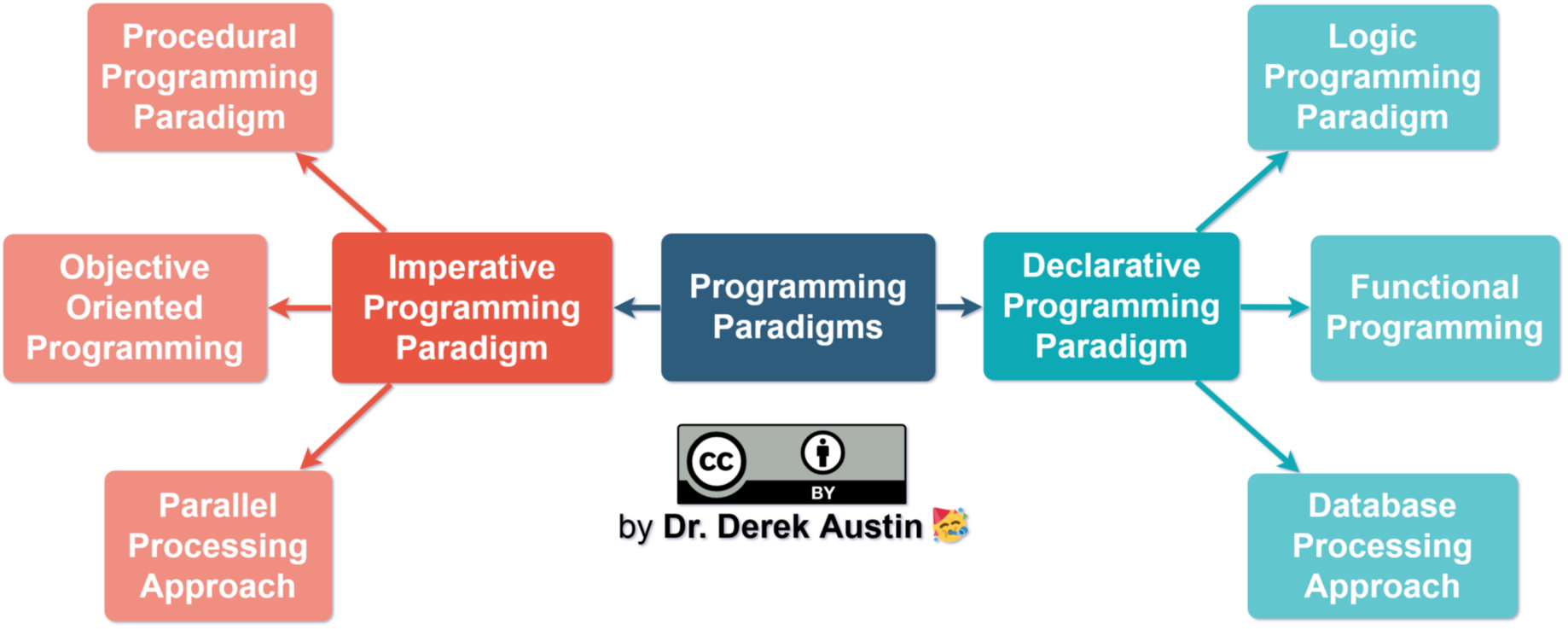
Programming Paradigms

Paradigm – In science, a paradigm describes distinct concepts or thought patterns in some scientific discipline.

Image source: https://javascript.plainenglish.io/what-are-javascript-programming-paradigms-3ef0f576dfdb

Imperative Programming

In imperative programming, we

• modify mutable variables,
• using assignments ( sets and/or re-sets the value stored in the storage location(s) denoted by a variable name)
• using control structures such as if-then-else, loops, break, continue, return.

Example: instruction sequences for a Von Neumann computer.

image source: https://diu-eil.gricad-pages.univ-grenoble-alpes.fr/archi-robotique-systeme-reseau/systeme/syst_2_processus.pdf

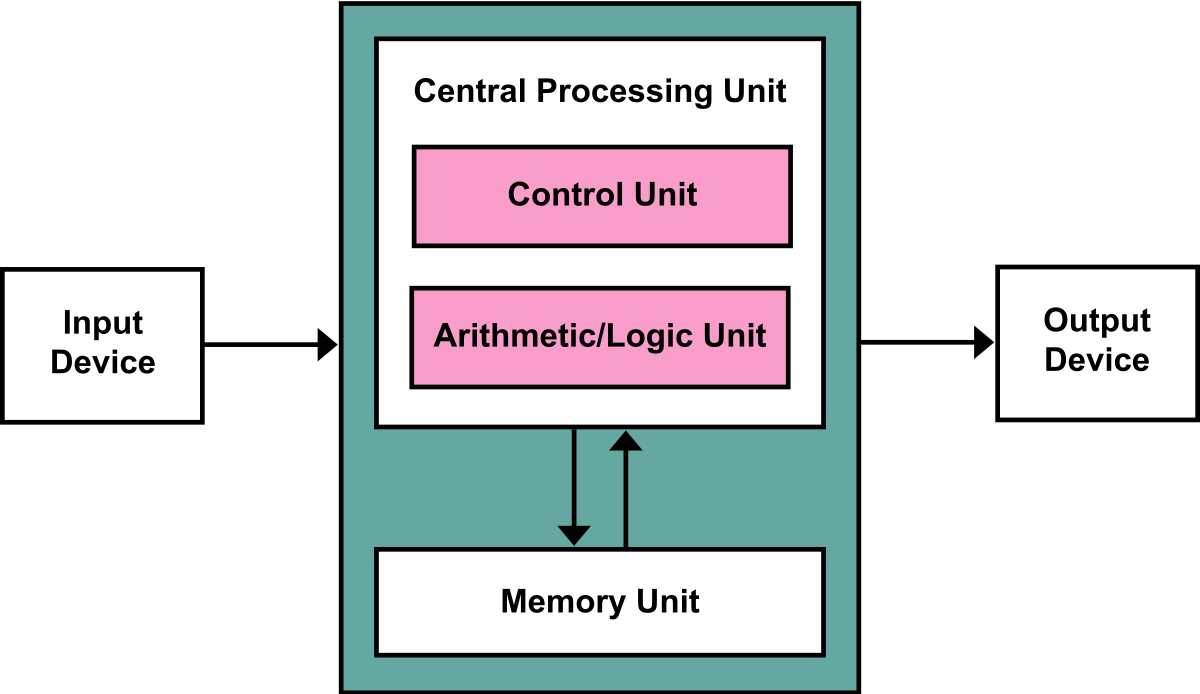
where

• Mutable variables ≈ memory cells
• Variable dereferences (used to access or manipulate data contained in the memory location pointed to by a pointer) ≈ load instructions
• Variable assignments ≈ store instructions
• Control structures ≈ jumps

Example: Complex Number Theory

Definition of Theory

A theory consists of

• one or more data types
• operations on these types
• laws that describe the relationships between values and operations

• Typically, a theory does not describe mutations.

image source: https://dandelife.com/what-are-the-things-you-should-know-about-complex-numbers/

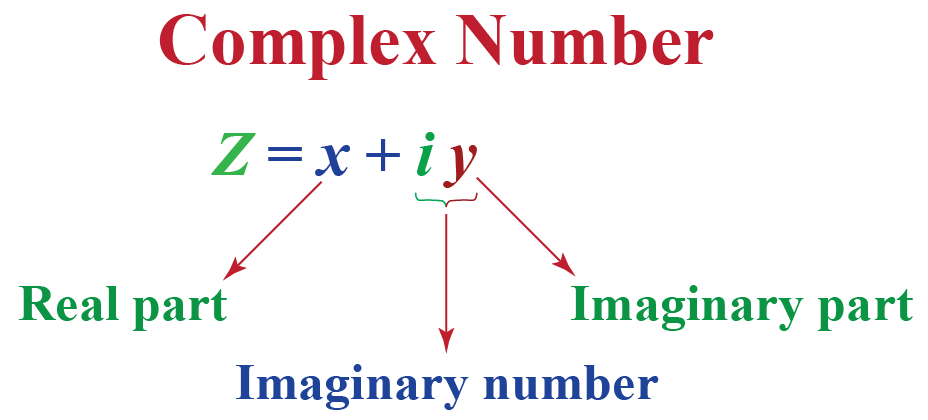
For instance, the theory of complex number defines the sum of two complex numbers by laws such as:

image source: https://numberworksheet.info/complex-number-multiplication-worksheet/

where complex numbers are addends

image source: https://www.greenemath.com/Prealgebra/5/PropertiesofAdditionLesson.html

Coding Example

In an imperative / mutable program, we can define ComplexNumber as :

class MutableComplexNumber(var real: Int, var imaginary: Int) {  
  // Change this complex number  
  def add(that: MutableComplexNumber) = {  
  real += that.real  
    imaginary += that.imaginary  
  }  
}

We can see that when adding two mutable complex numbers, the function will not return a new complex number. Instead, the original complex number (the addend) is changed.

import lecutreExample.MutableComplexNumber

class MutableComplexNumberTest extends munit.FunSuite {  
  test("when adding two mutable complex numbers," +  
    "will not get a new complex number ," +  
    "and the original numbers will be changed") {  
  val thisMutableComplexNumber = MutableComplexNumber(1, 2)  
  val thatMutableComplexNumber = MutableComplexNumber(3, 4)  
  thisMutableComplexNumber.add(thatMutableComplexNumber)  

  assertEquals(thisMutableComplexNumber.real, 4)  
  assertEquals(thisMutableComplexNumber.imaginary, 6)  
 }}

Issues

Issues of Mutation and Imperative Programming

In Math

There is no place for mutation if we implement high-level concepts following their mathematical theories.

• The theories do not admit it.
• Mutation can destroy useful laws in the theories.

In CS

The mutation changes an object and is one common side effect in programming languages.

• Mutation may lead to unexpected and hard-to-debug issues, where data becomes incorrect somewhere, and you have no idea where it happens.
• Mutation makes code harder to understand: at any time, an array or object may have a different value, so we need to be very careful when reading the code.
• Mutation of function arguments makes the behaviour of a function surprising.

Also, it’s hard to scale up ("Von Neumann" bottleneck)

• " One tends to conceptualize data structures word-by-word. "
• Need to define high-level abstractions such as collections, polynomials, geometric shapes, strings, documents

Functional Programming

Definition

Restricted : A functional programming language does not have

• mutable variables
• assignments,
• or imperative control structures.

Wider : a functional programming language focused on functions and immutable data structures.

FP Languages

• Lisp, Scheme, Racket, Clojure
• SML, Ocaml, F#
• Haskell
• Scala

Concepts and constructs from functional languages are also found in many traditional languages like Java.

Functions in FP

Functions in an FP language are first-class citizens i.e.

• they can be defined anywhere, including inside other functions
• like any other value, they can be passed as parameters to functions and returned as results
• as for other values, there exists a set of operators to compose functions
• i.e. functions can be values that are produced, consumed, and composed

Benefits

1. Reduce errors
   • no need to check two places to see all available variables

2. Increased developer productivity

   • Shorter code

3. More philosophical

   • More mathematical
   • Improve modularity
   • Higher-level abstractions

4. Morden

   • It is an effective tool to handle concurrency and parallelism on every scale
   • Our computers are not Van-Neuman machines anymore. They are parallel

Coding Example

In an functional / immutable program we can define ComplexNumber as :

class ImmutableComplexNumber(val real: Int, val imaginary: Int) {  
  // Return a new complex number  
  def add(that: ImmutableComplexNumber): ImmutableComplexNumber = {  
  new ImmutableComplexNumber(this.real + that.real, this.imaginary + that.imaginary)  
 }}

We can see that when adding two immutable complex numbers, the function will return a new complex number, and the original complex numbers (addends) will not change.

import lecutreExample.ImmutableComplexNumber  

class ImmutableComplexNumberTest extends munit.FunSuite {  
  test("when adding two immutable complex number," +  
    "will get a new complex number ," +  
    "and the original numbers won't change") {  
  val thisImmutableComplexNumber = ImmutableComplexNumber(1, 2)  
  val thatImmutableComplexNumber = ImmutableComplexNumber(3, 4)  
  val newImmutableComplexNumber = thisImmutableComplexNumber.add(thatImmutableComplexNumber)  
  assertEquals(newImmutableComplexNumber.real, 4)  
  assertEquals(newImmutableComplexNumber.imaginary, 6)  
  assertEquals(thisImmutableComplexNumber.real, 1)  
  assertEquals(thisImmutableComplexNumber.imaginary, 2)  
  assertEquals(thatImmutableComplexNumber.real, 3)  
  assertEquals(thatImmutableComplexNumber.imaginary, 4)  
 }}

Tool: REPL

Functional programming is a bit like using a calculator.

An interactive shell (or REPL, for Read-Eval-Print-Loop) lets one write expressions and responds with their value. Alternatively, you can use a scala worksheet.

Doc
REPL: https://docs.scala-lang.org/overviews/scala-book/scala-repl.html
Scala worksheet: https://docs.scala-lang.org/scala3/book/tools-worksheets.html

Example

The Scala REPL can be started by simply typing

> scala

Here are some simple interactions with the REPL

scala> 87 + 145 
res0: Int = 232 

Functional programming languages are more than simple calcululators because they let one define values and functions:

scala> def size = 2 
size: Int 

scala> 5 * size 
res1: Int = 10

Elements of Programming

Every non-trivial programming language provides:

• primitive* expressions representing the simplest elements
• ways to combine expressions
• ways to abstract expressions, which introduce a name for an expression that can be referred to.

Primitive

In Scala, Primitive types are similar to Java but are written capitalized:

Int	32-bit integers
Long	64-bit integers
Float	32-bit floating-point numbers
Double	64-bit floating-point numbers
Char	16-bit Unicode characters
Short	16-bit integers
Byte	8-bit integers
Boolean	boolean values true and false

Evaluation

A non-primitive expression is evaluated as follows.

1. Take the leftmost operator
2. Evaluate its operands (left before right)
3. Apply the operator to the operands

A name is evaluated by replacing it with the right-hand side of its definition.
The evaluation process stops once it results in a value.

Example： Circumference

// Circumference  
def pi = 3.14159  
def radius = 10  
(2 * pi) * radius

Scala worksheet output

def pi: Double
def radius: Int
val res0: Double = 62.8318

Parameters

Definitions can have parameters.

def square(x: Double) = x * x  

square(2)  
square(5 + 4)  
square(square(4))  

Output

def square(x: Double): Double

val res0: Double = 4.0
val res1: Double = 81.0
val res2: Double = 256.0

Function parameters come with their type, which is given after a colon.

def sumOfSquares(x: Double, y: Double) = square(x) + square(y)  

Applications of parameterized functions are evaluated similarly as operators:

1. Evaluate all function arguments, from left to right
2. Replace the function application by the function’s right-hand side, and, at the same time
3. Replace the formal parameters of the function with the actual arguments

sumOfSquares(3, 2+2)

it is converted to

-> sumOfSquares(3, 4) 
-> square(3) + square(4)
-> 9 + 16

Output

def sumOfSquares(x: Double, y: Double): Double
val res3: Double = 25

The substitution Model

Function Termination

Q: Does every expression reduce to a value (in a finite number of steps)?

No. Here is a counter-example

def loop: Int = loop loop

Substitution Model

This scheme of expression evaluation is called the substitution model, where

• all evaluation does is reduce an expression to a value.
• It can be applied to all expressions, as long as they have no side effects (storing files, printing, reading etc.).
• The substitution model is formalized in the λ-calculus, which gives a foundation for functional programming.

Functional Contract

• A method with a functional contract will always return the same value to the same arguments.
• Have no other side effects (like storing files, printing, reading).

• Thus, even if you mutate temporary values inside your function, it is still pure from the outside.

  Call-by-Name and Call-by-Value

Call-by-Value

The interpreter reduces function arguments to values before rewriting the function application.

def square(x:  Double ) = x * x
def sumOfSquares(x: Double, y: Double) = square(x) + square(y)  
sumOfSquares(3, 2+2) 
square(3) + square(2+2) 
3 * 3 + square(2+2) 
9 + square(2+2) 
9 + (2+2) * (2+2) 
9 + 4 * (2+2) 
9 + 4 * 4 
25

Call-by-Name

Apply the function to unreduced arguments.
We prepend => (rocket symbol) to its type.

def callByNameFunc(input: => InputType)  

def square(x: =>  Double ) = x*x
def sumOfSquares(x: => Double, y: => Double) = square(x) + square(y)  
sumOfSquares(3, 2+2) 
sumOfSquares(3, 4) 
square(3) + square(4) 
3 * 3 + square(4) 
9 + square(4) 
9 + 4 * 4 
9 + 16 
25

Comparison

Both strategies reduce to the same final values as long as

• the reduced expression consists of pure functions, and
• both evaluations terminate.

Performance

Say we have a function that takes two inputs and returns the square of the first input
i.e. the 2nd input is not used

def squareOfFirstElement(x: Int, y: Int) = x * x

Which one is faster? Call by name or call by value?

squareOfFirstElement(7, 8)  
squareOfFirstElement(3+4, 8) 
squareOfFirstElement(7, 2*4)  
squareOfFirstElement(3+4, 2*4)  

We want to examine the evaluation strategy and determine which one is faster (fewer steps) in these conditions:

Scenario 1

squareOfFirstElement(2,3)

call by value:

squareOfFirstElement(2,3) 
↓ 
2*2 
↓
4  

call by name:

squareOfFirstElement(2,3) 
↓
2*2 
↓
4  

Here the result is reached with the same number of steps.

Senario 2

squareOfFirstElement(3+4,8)

call by value:

squareOfFirstElement(7,8) 
↓ 
7*7
↓ 
49  

call by name:

(3+4)*(3+4) 
↓
7*(3+4)
↓
7*7 
↓
49  

Here call by value is faster.

Senario 3

squareOfFirstElement(7,2*4)

call by value:

squareOfFirstElement(7,8) 
↓ 
7*7 
↓
49

call by name:

7 * 7 
↓ 
49  

Here call by name is faster.

Senario 4

squareOfFirstElement(3+4, 2*4) 

call by value:

squareOfFirstElement(7,2*4) 
↓ 
squareOfFirstElement(7, 8)
↓
7*7 
↓
49  

call by name:

(3+4)*(3+4)
↓
7*(3+4) 
↓ 
7*7
↓ 
49  

The result is reached within the same steps.

Advantage

Call-by-value

• it evaluates every function argument only once
• avoids the repeated re-computation of argument expressions

Call-by-name

• a function argument is not evaluated if the corresponding parameter is unused in the evaluation of the function body.

Termination

Call-by-name and call-by-value evaluation strategies reduce an expression to the same value as long as both evaluations terminate.

Q: But what if termination is not guaranteed?

If CBV evaluation of an expression #e terminates, then CBN evaluation of #e terminates, too.
The other direction is not true.

Terminates?	CallByName	CallByValue	Possible?
1	T	T	T
2	F	T	F
3	F	F	T
4	T	F	T

For example: find an expression that terminates under CBN but not under CBV.

def firstByValue(x: Int, y: Int) = x  
def firstByName(x: => Int, y: => Int) = x  

def loop: Int = {  
  while (true) {  
    Thread.sleep(1000)  
  }  
  1  
}  

// #loop never called，
firstByName(1, loop)  
// Return: val res0: Int = 1

// Whill try to exe #loop first 
firstByValue(1, loop) 
// Never end