(1) Parallel programming
About
:octocat: GitHub: All of the example code: repo (link)
:page_facing_up: blog link: https://purrgramming.life/cs/os/parallel :star:
These are my lecture notes and the code for Coursera online course Parallel programming (Scala 2 version) (Week1) from École Polytechnique Fédérale de Lausanne (EPFL)
Why is parallel programming important to learn?
Paralleled programming is becoming more and more critical. Almost every desktop computer, laptop, or handheld device is equipped with multi-core processors and can execute computations in parallel. Therefore, it is more important than ever to harness these resources.
Definition
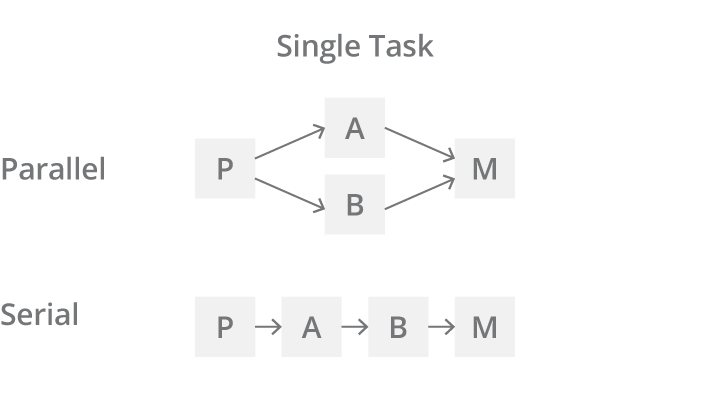
Parallel computing is a type of computation in which many calculations are performed at the same time.
Parallel computing provides computational power when
sequential computing cannot do so
Parallel vs. Concurrent
| Parallel | Concurrent | |
|---|---|---|
| Def | Uses parallel hardware to execute computation more quickly. | May or may not execute multiple executions at the same time |
| Benefit | Efficiency | Modularity, Responsiveness, Maintainability |
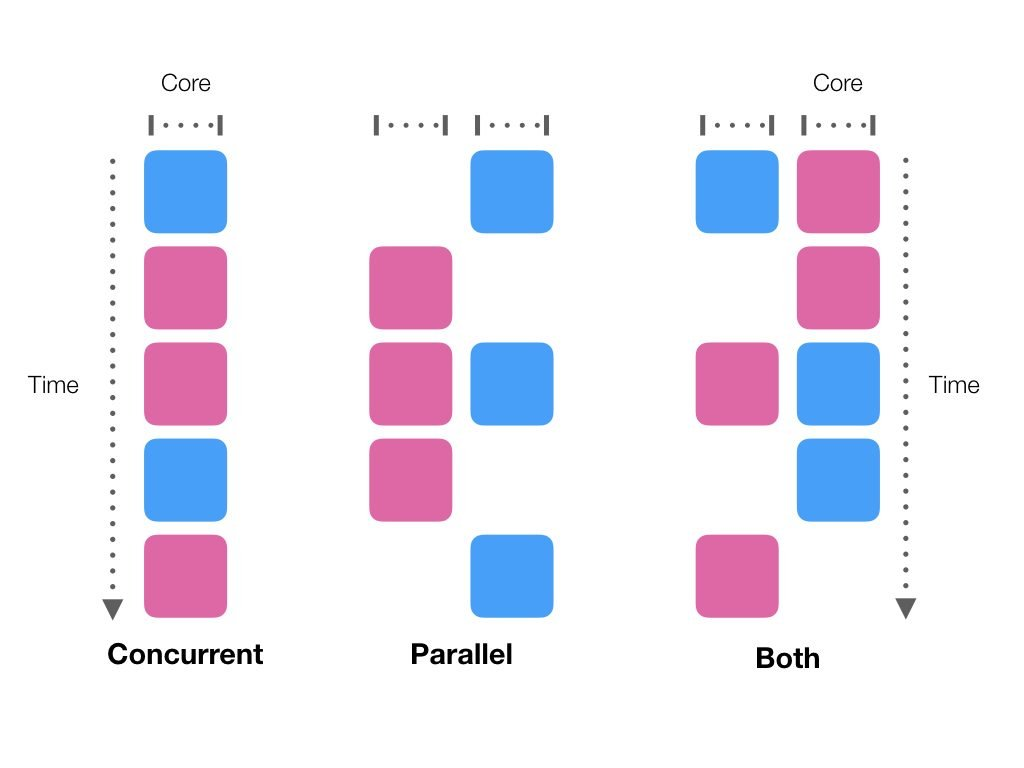

Basic principle
- computation can be divided into smaller subproblems
- each of which can be solved simultaneously
Underneath the Hood
Q: What happens inside a system when we use parallel? Efficient parallelism requires support from
- language and libraries
- virtual machine (such as Java Virtual Machine)
- operating system
- hardware
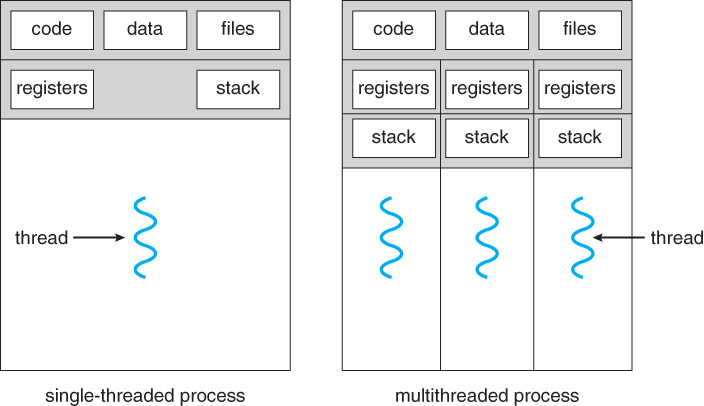
Thread and Process
Process
The process is an instance of a program executing in the OS.
- The same program can be started as a process more than once or simultaneously in the same OS.
- The operating system multiplexes many different processes and a limited number of CPUs to get time slices of execution. This mechanism is called multitasking.
- Two different processes cannot directly access each other’s memory – they are isolated.
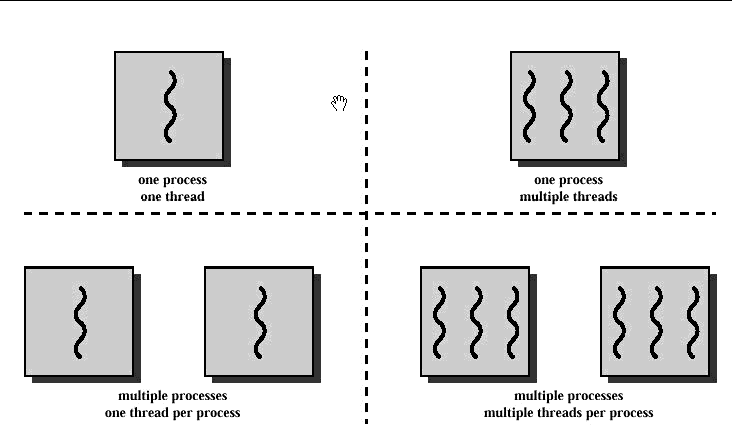
Thread
Each process can contain multiple independent concurrency units called threads.
Each thread in JVM is created and controlled by a unique object of the java.lang.Thread class.
- Threads can be started from within the same program, and they share the same memory address space.
- Each thread has a program counter and a program stack.
- JVM threads cannot modify each other’s stack memory. They can only modify the heap memory.
!
Main Thread
A user thread is automatically created to execute the main() method, i.e., the main thread.
Thread vs. Process

Thread states
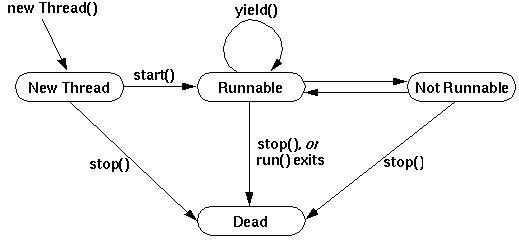
See this ref for more info – Thread States
thread.join
Join is a synchronization method that blocks the calling thread (that is, the thread that calls the method) until the thread whose join method is completed.
- Use this method to ensure that a thread has been terminated.
- The caller will block indefinitely if the thread does not terminate.

Other Terms
Operating system
Software that manages hardware and software resources and schedules program execution.
Parallelism Granularity
Parallelism manifests itself at different granularity levels.
- bit-level parallelism – processing multiple bits of data in parallel
- instruction-level parallelism – executing different instructions from the
same instruction stream in parallel - task-level parallelism – executing separate instruction streams in
parallel
Creating and starting threads
Each JVM process starts with the main thread.
To start other threads:
- Define a Thread subclass.
- Instantiate a new Thread object.
- Call start on the Thread object.
The Thread subclass defines the thread’s code (hello world).
The same custom Thread subclass can be used to start multiple threads.
class HelloWorld extends Thread {
override def run(): Unit = {
println("Hello world!")
}}
object SingleThread extends App {
val t = new HelloThread
t.start()
t.join()
}Sys output
Hello, world!Atomicity
An operation is atomic if it appears as if it occurred instantaneously from the point of view of other threads.
Overlap Examples
The issue that atomicity can fix: Separate statements in two threads can overlap
class HelloWorldA extends Thread {
override def run(): Unit = {
println("A1 Hello world!")
println("A2 Hello world!")
println("A3 Hello world!")
}
}
class HelloWorldB extends Thread {
override def run(): Unit = {
println("B1 Hello world!")
println("B2 Hello world!")
println("B3 Hello world!")
}
}
object MultiThreadWithOverlap extends App {
val tA = new HelloWorldA
val tB = new HelloWorldB
tA.start()
tB.start()
tA.join()
tB.join()
}Sys output
A1 Hello world!
A2 Hello world!
B1 Hello world!
A3 Hello world!
B2 Hello world!
B3 Hello world!In some cases, we want to ensure that a sequence of statements in a specific thread executes at once.
object MultiThreadWithOverlap2 extends App {
var uidCount = 0L
def startThread() = {
val t = new Thread {
override def run(): Unit = {
val uids = for (i <- 1 to 10) yield getUniqueId()
println(uids)
}
}
t.start()
t
}
def getUniqueId(): Long = {
uidCount = uidCount + 1
uidCount
}
startThread()
startThread()
}
Sys output
Vector(1, 2, 4, 6, 8, 10, 12, 13, 15, 17)
Vector(1, 3, 5, 7, 9, 11, 12, 14, 16, 17)Synchronized Block
Threads within a given process share the same memory space
- pros: Enable data sharing
- cons: Threads might modify the same resource at the same time
Access Control: Code block after a synchronized call on an object x is never executed by two threads at the same time
i.e. Change the getUniqueId to
val x = new AnyRef {}
def getUniqueId(): Long = x.synchronized {
uidCount = uidCount + 1
uidCount
}Full code
object SynchronizeExample extends App {
val x = new AnyRef {}
var uidCount = 0L
def startThread()
= {
val t = new Thread {
override def run(): Unit = {
val uids = for (i <- 1 to 10) yield getUniqueId()
println(uids)
}
}
t.start()
t
}
def getUniqueId(): Long = x.synchronized {
uidCount = uidCount + 1
uidCount
}
startThread()
startThread()
}
Sys output
Vector(2, 12, 13, 14, 15, 16, 17, 18, 19, 20)
Vector(1, 3, 4, 5, 6, 7, 8, 9, 10, 11)Where we can see that
- Different threads use the synchronized block to agree on unique values.
- The synchronized block is an example of synchronization primitive.
Nesting Synchronized Block
Invocations of the synchronized block can nest
like
package week1.LectureExample
object SynchronizeExample extends App {
val x = new AnyRef {}
var uidCount = 0L
def startThread() = {
val t = new Thread {
override def run(): Unit = {
val uids = for (i <- 1 to 10) yield getUniqueId()
println(uids)
}
}
t.start()
t
}
def getUniqueId(): Long = x.synchronized {
uidCount = uidCount + 1
uidCount
}
startThread()
startThread()
}
Memory model
A memory model is a set of rules that describes how threads interact when accessing shared memory.
Java Memory Model is the memory model for the JVM.
- Two threads writing to separate locations in memory do not need synchronization.
- A thread
Xcallsjoinon another threadYis guaranteed to observe all the writes by threadYafter #join returns.
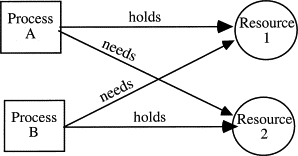
Deadlock
Definition
Deadlock: a thread is waiting for an object lock that another thread holds, and this second thread is waiting for an object lock that the first thread holds
i.e. each thread is waiting for the other thread to relinquish a lock and wait forever
Condition
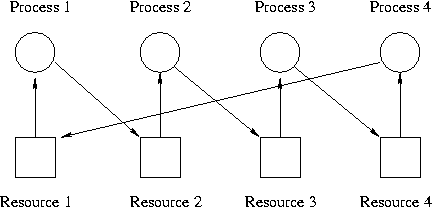
- Mutual exclusion: At least one resource must be held in a non-shareable mode; that is, only one process at a time can use the resource.
- Hold and wait or resource holding: a process currently holding at least one resource and requesting additional resources held by other processes.
- No preemption: a resource can be released only voluntarily by the process holding it.
- Circular wait: each process must be waiting for a resource held by another process, which in turn is waiting for the first process to release the resource.
Deadlock Code Example
The amount of money in a bank account is locked (synchronized) when transferring money to ensure that the number is correct. If we have two accounts, and both are trying to send money to each other, then both accounts are locked.
Here, the two transfer threads compete for resources
(amount in the Account), and wait for each to finish without releasing
the already acquired resources.
package week1.LectureExample
// Program will sometimes terminate.
class Account(var balance: Int = 0) {
def sendMoney(receiver: DeadlockFreeAccount, n: Int) = {
this.synchronized {
receiver.synchronized {
this.balance -= n
receiver.balance += n
}
}
}
}
object DeadlockExample extends App {
val account1 = new DeadlockFreeAccount(2000)
val account2 = new DeadlockFreeAccount(1000)
// account 1 -> account 2, and
// account 2 -> account 1
val transfer1 = transferThread(account1, account2, 20)
val transfer2 = transferThread(account2, account1, 20)
transfer1.join()
transfer2.join()
def transferThread(sender: DeadlockFreeAccount, receiver: DeadlockFreeAccount, amount: Int) = {
val t = new Thread {
override def run(): Unit = {
// Loop: make it easier to trigger deadlock
for (i <- 0 until amount) {
sender.sendMoney(receiver, 1)
}
println(s"After transfer: sender account: ${sender.balance} , receiver " +
s"account:${receiver.balance}")
}
}
t.start()
t
}
}
Result:
The app would never end.Deadlock Handling
OS
- Most current operating systems cannot prevent deadlocks.
- When a deadlock occurs, different operating systems respond to them in different non-standard manners.
- Most approaches work by preventing the fourth condition (Circular wait)
Ignoring deadlock
Ostrich algorithm:
- In this approach, it is assumed that a deadlock will never occur.
- Initially used by UNIX.
- Used when the time intervals between occurrences of deadlocks are large and the data loss incurred each time is tolerable.
- Can be safely done if deadlocks are formally proven never to occur.
Deadlock Prevention vs Deadlock Avoidance
Deadlock prevention – ensure that at least one of the necessary conditions for deadlock can never occur.
Deadlock avoidance – ensure that the system does not enter an unsafe state.

Deadlock Prevention
Summary
| Condition | Approach | Practical? |
|---|---|---|
| Mutual Exclusion | Spooling | x |
| Hold and Wait | Request for all the resources initially | x |
| No Preemption | Snatch all the resources | x |
| Circular Wait | Assign priority to each resource and order resources numerically | yes |
Details
-
Removing the mutual exclusion condition means that no process will have exclusive access to a resource.
- Algorithm: non-blocking synchronization algorithms.
- Not practical:
- This proves impossible for resources that cannot be spooled.
- But even with spooled resources, the deadlock could still occur.
-
The hold and wait or resource holding condition: These algorithms, such as serializing tokens, are all-or-none algorithms.
Algorithm 1: may be removed by requiring processes to request all the resources they will need before starting up or embarking upon a particular set of operations.
Not practical:- This advanced knowledge is frequently difficult to satisfy
- This is an inefficient use of resources.
Algorithm 2: require processes to request resources only when it has none;
Not practical:- Threads must release all their currently held resources before requesting all the resources they will need from scratch. However, resources may be allocated and remain unused for long periods.
- A process requiring a popular resource may have to wait indefinitely, as such a resource may always be allocated to some process, resulting in resource starvation.
-
The no preemption condition: inability to enforce preemption may interfere with a priority algorithm.
Not practical:
- A process must have a resource for a certain amount of time, or the processing outcome may be inconsistent, or thrashing may occur.
- Preemption of a "locked out" resource generally implies a rollback and is to be avoided since it is a very costly overhead.
Algorithms
- lock-free
- wait-free
- optimistic concurrency control
- The circular wait condition:
Algorithms- Disabling interrupts during critical sections and using a hierarchy to determine a partial ordering of resources. If no obvious hierarchy exists, even the memory address of resources has been used to determine ordering and resources are requested in the increasing order of the enumeration.
- Dijkstra
Deadlock avoidance
Deadlock avoidance does not impose any conditions as seen in prevention, but each resource request is carefully analyzed to see whether it could be safely fulfilled without causing deadlock.
Deadlock avoidance requires that the operating system be given additional information concerning which resources a process will request and use during its lifetime.
Algorithm: Banker’s algorithm: analyzes each request by examining that there is no possibility of deadlock occurrence in the future if the requested resource is allocated.
Drawback: its requirement of information in advance about how resources are to be requested in the future. One of the most used deadlock avoidance algorithms is
Deadlock Solution Code Example
For the example we used in the deadlock Code example, one approach is always to acquire resources in the same order. This assumes an ordering relationship on the resources.
package week1.LectureExample
// Program will sometimes terminate.
class Account(var balance: Int = 0) {
def sendMoney(receiver: DeadlockFreeAccount, n: Int) = {
this.synchronized {
receiver.synchronized {
this.balance -= n
receiver.balance += n
}
}
}
}
object DeadlockExample extends App {
val account1 = new DeadlockFreeAccount(2000)
val account2 = new DeadlockFreeAccount(1000)
// account 1 -> account 2, and
// account 2 -> account 1
val transfer1 = transferThread(account1, account2, 20)
val transfer2 = transferThread(account2, account1, 20)
transfer1.join()
transfer2.join()
def transferThread(sender: DeadlockFreeAccount, receiver: DeadlockFreeAccount, amount: Int) = {
val t = new Thread {
override def run(): Unit = {
// Loop: make it easier to trigger deadlock
for (i <- 0 until amount) {
sender.sendMoney(receiver, 1)
}
println(s"After transfer: sender account: ${sender.balance} , receiver " +
s"account:${receiver.balance}")
}
}
t.start()
t
}
}
Sys output
After transfer: sender account: 2000 , receiver account:1000
After transfer: sender account: 980 , receiver account:2020
Process finished with exit code 0Designing Computations in Parallel
Basic Parallel Construct
Given expressions e1 and e2, compute them in parallel and return the pair of results.
parallel(e1, e2)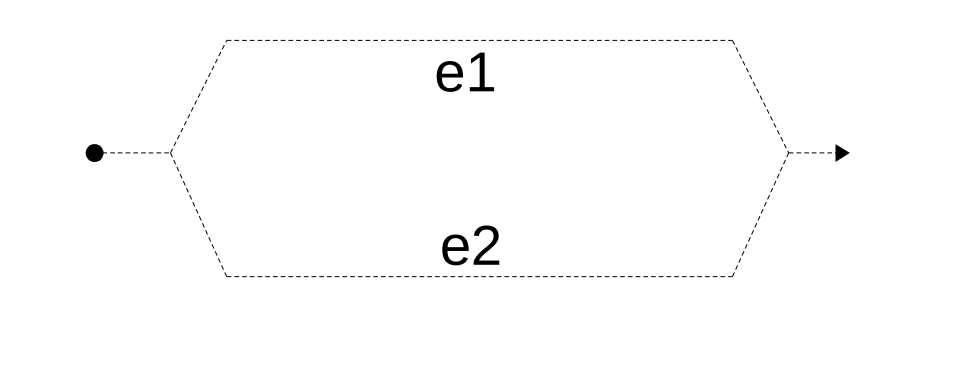
where we can solve the subproblems in parallel
Head Up
Will have a separate blog for the implementation of #parallel
If you want to run the example code, you can copy the definition of #parallel from https://github.com/Victoria-Pinzhen-Liao/parallel-programming/blob/main/src/main/scala/week1/LectureExample/package.scala

Example: p-norm
Given a vector as an array (of integers), compute its p-norm.
Where: the function p-norm. A p-norm is a generalization of the notion of length from geometry.

Subtask (The Main Step)
The subtask (main step) is to compute the sum of the elements the array raised to p.
Let us define a slightly more general function, called sum segment. i.e. solve sequentially the following sumSegment problem: given
- an integer array
a, representing our vector - a positive double floating-point number
p - start index of the segment as well as the end boundary, an index before which we should stop summing up -two valid indices
s <= tinto the arraya
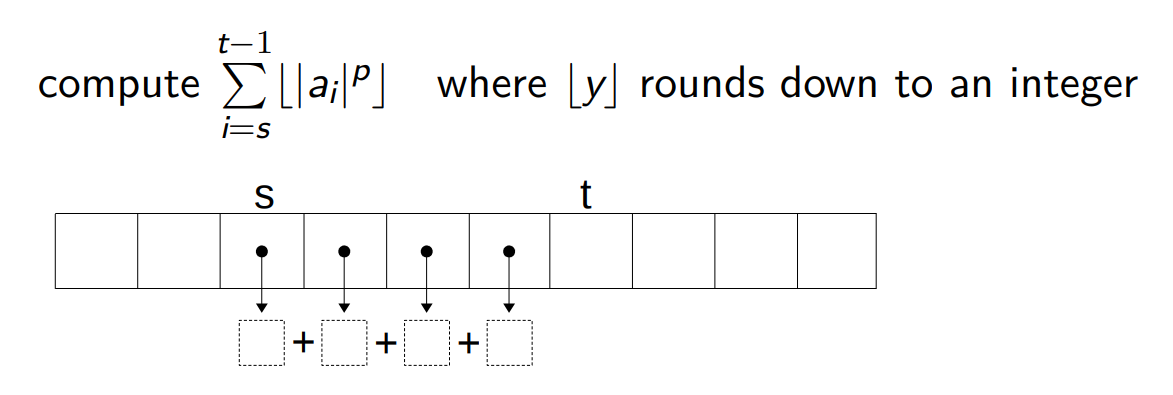
The solution is just a traversal of the array that adds up the powers of elements. We use a while loop to do the traversal. The power function is a simple combination of the appropriate math library functions.
def sumSegment(a: Array[Int], p: Double, s: Int, t: Int): Int = {
var i = s
var sum: Int = 0
while (i < t) {
sum = sum + power(a(i), p)
i = i + 1
}
sum
}
def power(x: Int, p: Double): Int = math.exp(p * math.log(abs(x))).toIntP Norm Computation
Q: Now that we have the sum segment function, how do we compute the p-norm?We apply sumSegment to the entire array, from index zero to the array's length. We then raise the result to the power one over p. This gives us a sequential version for computing the p-norm.

def pNorm(a: Array[Int], p: Double): Int = {
power(sumSegment(a, p, 0, a.size), 1 / p)
}Full code
package week1.LectureExample
import week1.LectureExample.PNormCalculator.pNorm
import scala.math.abs
object PNorm extends App {
val array = Array(1, 2, 3, 4, 5, 6, 7, 8)
val p = 2.5
pNorm(array, p)
}
object PNormCalculator {
def pNorm(a: Array[Int], p: Double): Int = {
val result = power(sumSegment(a, p, 0, a.size), 1 / p)
println(s"The p norm of ${a.toSeq} (p = $p) is: $result")
result
}
def sumSegment(a: Array[Int], p: Double, s: Int, t: Int): Int = {
var i = s
var sum: Int = 0
while (i < t) {
sum = sum + power(a(i), p)
i = i + 1
}
sum
}
def power(x: Int, p: Double): Int = math.exp(p * math.log(abs(x))).toInt
}Sys output
The p norm of ArraySeq(1, 2, 3, 4, 5, 6, 7, 8) (p = 2.5) is: 12Split P Norm Computation into 2 Calcs (Sequencial)
Q: How do we go from here to a parallel version?Now, observe that the summation can be expressed in two parts:
- sum up to some middle element
m, - sum from that middle element to the end.
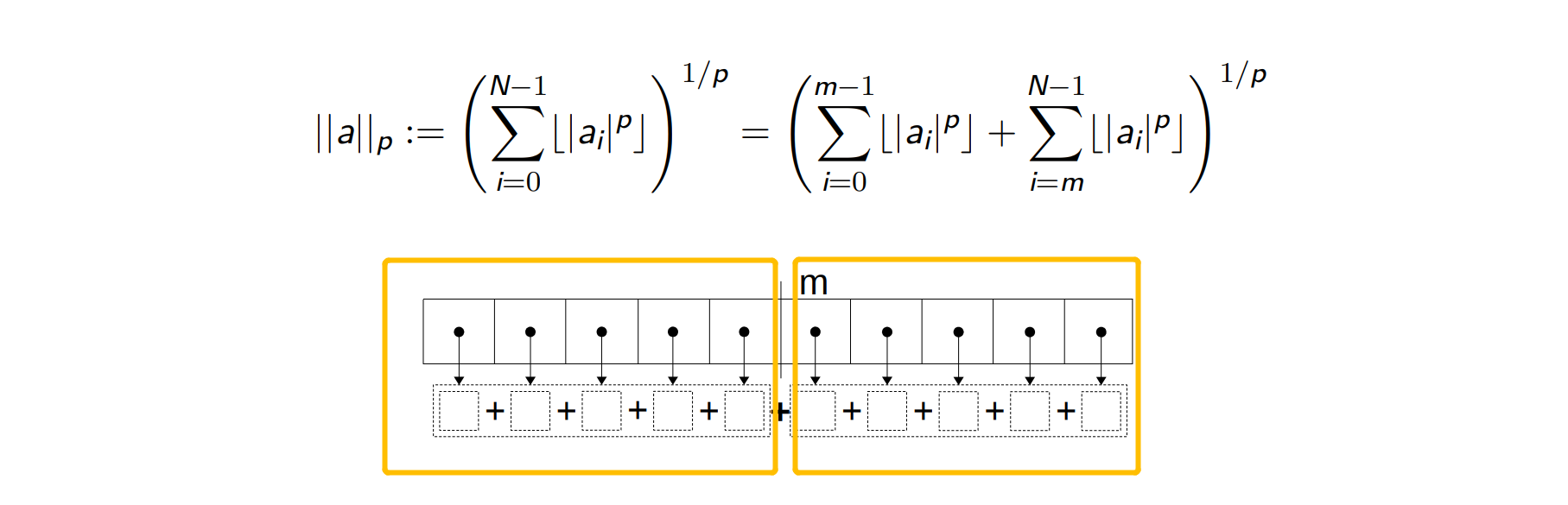
Q: What is a Scala expression that corresponds to using two sums?We need to invoke the sum segment twice, then add up the two intermediate sums before raising everything to the power of one over p.
// Sequential
def sequentialPNormCalc(a: Array[Int], p: Double): Int = {
val m = a.length / 2
val (sum1, sum2) = (sumSegment(a, p, 0, m),
sumSegment(a, p, m, a.length))
val result = power(sum1 + sum2, 1 / p)
println(s"The p norm of ${a.toSeq} is: $result")
result
}Full code:
package week1.LectureExample
import week1.LectureExample.PNormCalculator.{power, sumSegment}
import week1.LectureExample.SequentialPNormCalculator._
object SequentialPNormCalc extends App {
val array = Array(1, 2, 3, 4, 5, 6, 7, 8)
val p = 2.5
sequentialPNormCalc(array, p)
}
object SequentialPNormCalculator {
def sequentialPNormCalc(a: Array[Int], p: Double): Int = {
val m = a.length / 2
val (sum1, sum2) = (sumSegment(a, p, 0, m),
sumSegment(a, p, m, a.length))
val result = power(sum1 + sum2, 1 / p)
println(s"The p norm of ${a.toSeq} is: $result")
result
}
}Sys output
The p norm of ArraySeq(1, 2, 3, 4, 5, 6, 7, 8) (p = 2.5) is: 12Split P Norm Computation into 2 Calcs (Parallel)
Q: This is still sequential computation. How do we make it parallel?
All we need to do is wrap the pair into the parallel construct.
// Parallel
def parallelPNormCalc(a: Array[Int], p: Double): Int = {
val m = a.length / 2
val (sum1, sum2) = parallel(sumSegment(a, p, 0, m),
sumSegment(a, p, m, a.length))
val result = power(sum1 + sum2, 1 / p)
println(s"The p norm of ${a.toSeq} is: $result")
result
}
Full Code
package week1.LectureExample
import week1.LectureExample.PNormCalculator.{power, sumSegment}
import week1.LectureExample.ParallelPNormCalculator.parallelPNormCalc
object ParallelPNormCalc extends App {
val array = Array(1, 2, 3, 4, 5, 6, 7, 8)
val p = 2.5
parallelPNormCalc(array, p)
}
object ParallelPNormCalculator {
// Parallel
def parallelPNormCalc(a: Array[Int], p: Double): Int = {
val m = a.length / 2
val (sum1, sum2) = parallel(sumSegment(a, p, 0, m),
sumSegment(a, p, m, a.length))
val result = power(sum1 + sum2, 1 / p)
println(s"The p norm of ${a.toSeq} is: $result")
result
}
}Sys output
The p norm of ArraySeq(1, 2, 3, 4, 5, 6, 7, 8) (p = 2.5) is: 12Given a platform that supports parallel execution, the computation with parallel may run up to twice as fast as the one without parallelism.
The parallel version may take some time to set up parallel execution, but after that might make progress on processing array elements twice as fast as the sequential one.
Split P Norm Computation into 4 Calcs (Parallel)
Q: Suppose that we have at least four parallel hardware threads. How would we process four array segments in parallel using our parallel construct?
We divide the array into four segments. We can compute the sum of the first two segments in parallel and the sum of the second two segments in parallel.
Finally, these two parallel computations of pairs can take place in parallel. Once we get four partial sums, we can add up these four.
val m = a.length / 2
val m1 = a.length / 4;
val m2 = a.length / 2;
val m3 = 3 * a.length / 4
val ((sum1, sum2), (sum3, sum4)) =
parallel(parallel(sumSegment(a, p, 0, m1), sumSegment(a, p, m1, m2)),
parallel(sumSegment(a, p, m2, m3), sumSegment(a, p, m3, a.length)))
power(sum1 + sum2 + sum3 + sum4, 1 / p)
Split P Norm Computation Recursively (Parallel)
Q: Is there a recursive algorithm for an unbounded number of threads?We can define segmentRec, which uses parallelism, to sum up, a given segment of the array. When the segment size is 1, it computes the sum sequentially. Otherwise, it divides the segment in half and invokes itself recursively on two smaller segments.
package week1.LectureExample
import week1.LectureExample.PNormCalculator.{power, sumSegment}
import week1.LectureExample.ParallelPNormCalculatorWithRecursion.pNormRecursion
object ParallelPNormCalcWithRecursion extends App {
val array = Array(1, 2, 3, 4, 5, 6, 7, 8)
val p = 2.5
pNormRecursion(array, p)
}
object ParallelPNormCalculatorWithRecursion {
def pNormRecursion(a: Array[Int], p: Double): Int = {
val result = power(sumSegmentRecursive(a, p, 0, a.length, 2), 1 / p)
println(s"The p norm of ${a.toSeq} is: $result")
result
}
// like sumSegment but parallel and recursive
def sumSegmentRecursive(a: Array[Int], p: Double, s: Int, t: Int, threshold: Int): Int = {
if (t - s < threshold)
sumSegment(a, p, s, t) // small segment: do it sequentially
else {
val m = s + (t - s) / 2
val (sum1, sum2) = parallel(sumSegmentRecursive(a, p, s, m, threshold),
sumSegmentRecursive(a, p, m, t, threshold))
sum1 + sum2
}
}
}