(1) Principles of Functional Programming
About
:octocat: GitHub: All of the example code: repo (link)
:page_facing_up: blog link: https://purrgramming.life/cs/programming/fp/ :star:
Programming Paradigms
Paradigm – In science, a paradigm describes distinct concepts or thought patterns in some scientific discipline.
Image source: https://javascript.plainenglish.io/what-are-javascript-programming-paradigms-3ef0f576dfdb
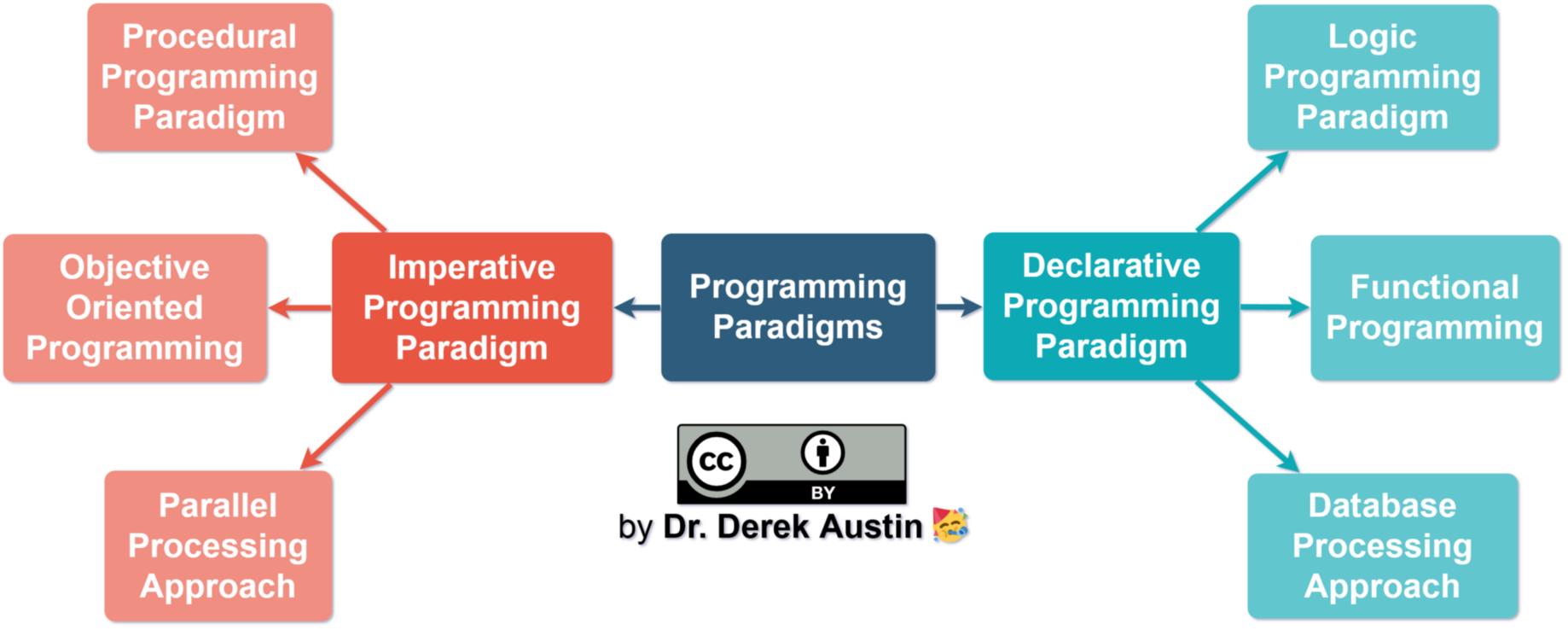
Imperative Programming
In imperative programming, we
- modify mutable variables,
- using assignments ( sets and/or re-sets the value stored in the storage location(s) denoted by a variable name)
- using control structures such as if-then-else, loops, break, continue, return.
Example: instruction sequences for a Von Neumann computer.
image source: https://diu-eil.gricad-pages.univ-grenoble-alpes.fr/archi-robotique-systeme-reseau/systeme/syst_2_processus.pdf
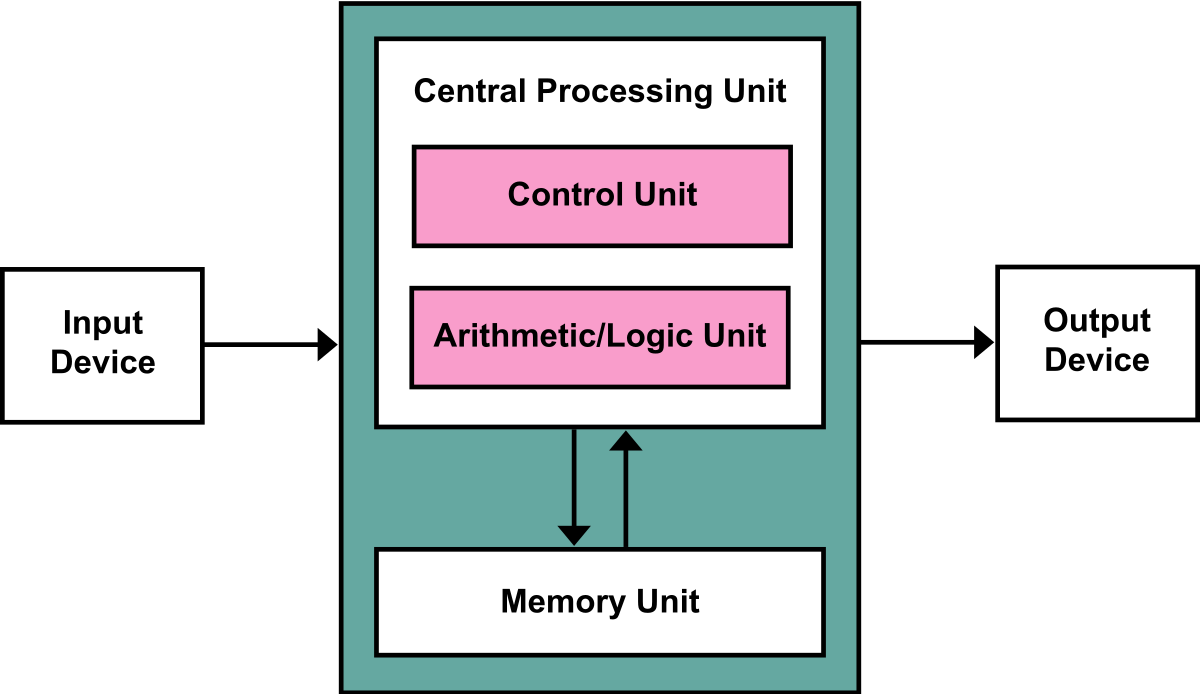
where
- Mutable variables ≈ memory cells
- Variable dereferences (used to access or manipulate data contained in the memory location pointed to by a pointer) ≈ load instructions
- Variable assignments ≈ store instructions
- Control structures ≈ jumps
Example: Complex Number Theory
Definition of Theory
A theory consists of
- one or more data types
- operations on these types
- laws that describe the relationships between values and operations
-
Typically, a theory does not describe mutations.
image source: https://dandelife.com/what-are-the-things-you-should-know-about-complex-numbers/
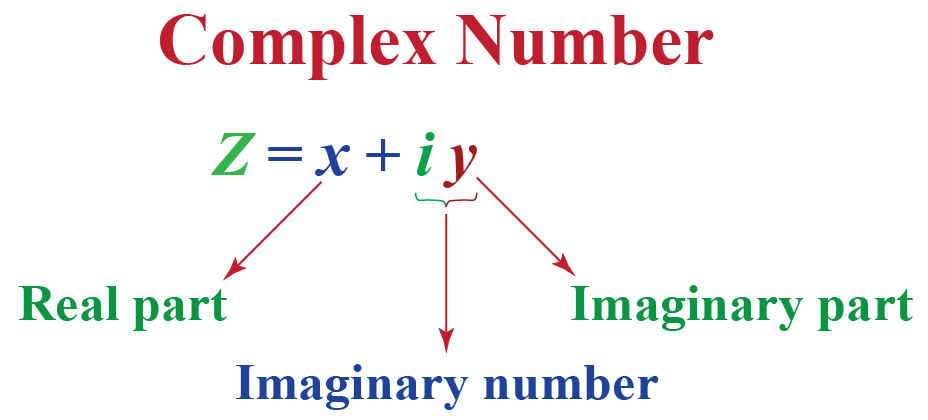
For instance, the theory of complex number defines the sum of two complex numbers by laws such as:
image source: https://numberworksheet.info/complex-number-multiplication-worksheet/

where complex numbers are addends
image source: https://www.greenemath.com/Prealgebra/5/PropertiesofAdditionLesson.html
Coding Example
In an imperative / mutable program, we can define ComplexNumber as :
class MutableComplexNumber(var real: Int, var imaginary: Int) {
// Change this complex number
def add(that: MutableComplexNumber) = {
real += that.real
imaginary += that.imaginary
}
}We can see that when adding two mutable complex numbers, the function will not return a new complex number. Instead, the original complex number (the addend) is changed.
import lecutreExample.MutableComplexNumber
class MutableComplexNumberTest extends munit.FunSuite {
test("when adding two mutable complex numbers," +
"will not get a new complex number ," +
"and the original numbers will be changed") {
val thisMutableComplexNumber = MutableComplexNumber(1, 2)
val thatMutableComplexNumber = MutableComplexNumber(3, 4)
thisMutableComplexNumber.add(thatMutableComplexNumber)
assertEquals(thisMutableComplexNumber.real, 4)
assertEquals(thisMutableComplexNumber.imaginary, 6)
}}Issues
Issues of Mutation and Imperative Programming
In Math
There is no place for mutation if we implement high-level concepts following their mathematical theories.
- The theories do not admit it.
- Mutation can destroy useful laws in the theories.
In CS
The mutation changes an object and is one common side effect in programming languages.
- Mutation may lead to unexpected and hard-to-debug issues, where data becomes incorrect somewhere, and you have no idea where it happens.
- Mutation makes code harder to understand: at any time, an array or object may have a different value, so we need to be very careful when reading the code.
- Mutation of function arguments makes the behaviour of a function surprising.
Also, it’s hard to scale up ("Von Neumann" bottleneck)
- " One tends to conceptualize data structures word-by-word. "
- Need to define high-level abstractions such as collections, polynomials, geometric shapes, strings, documents
Functional Programming
Definition
Restricted : A functional programming language does not have
- mutable variables
- assignments,
- or imperative control structures.
Wider : a functional programming language focused on functions and immutable data structures.
FP Languages
- Lisp, Scheme, Racket, Clojure
- SML, Ocaml, F#
- Haskell
- Scala
Concepts and constructs from functional languages are also found in many traditional languages like Java.
Functions in FP
Functions in an FP language are first-class citizens i.e.
- they can be defined anywhere, including inside other functions
- like any other value, they can be passed as parameters to functions and returned as results
- as for other values, there exists a set of operators to compose functions
- i.e. functions can be values that are produced, consumed, and composed
Benefits
- Reduce errors
- no need to check two places to see all available variables
-
Increased developer productivity
- Shorter code
-
More philosophical
- More mathematical
- Improve modularity
- Higher-level abstractions
-
Morden
- It is an effective tool to handle concurrency and parallelism on every scale
- Our computers are not Van-Neuman machines anymore. They are parallel
Coding Example
In an functional / immutable program we can define ComplexNumber as :
class ImmutableComplexNumber(val real: Int, val imaginary: Int) {
// Return a new complex number
def add(that: ImmutableComplexNumber): ImmutableComplexNumber = {
new ImmutableComplexNumber(this.real + that.real, this.imaginary + that.imaginary)
}}We can see that when adding two immutable complex numbers, the function will return a new complex number, and the original complex numbers (addends) will not change.
import lecutreExample.ImmutableComplexNumber
class ImmutableComplexNumberTest extends munit.FunSuite {
test("when adding two immutable complex number," +
"will get a new complex number ," +
"and the original numbers won't change") {
val thisImmutableComplexNumber = ImmutableComplexNumber(1, 2)
val thatImmutableComplexNumber = ImmutableComplexNumber(3, 4)
val newImmutableComplexNumber = thisImmutableComplexNumber.add(thatImmutableComplexNumber)
assertEquals(newImmutableComplexNumber.real, 4)
assertEquals(newImmutableComplexNumber.imaginary, 6)
assertEquals(thisImmutableComplexNumber.real, 1)
assertEquals(thisImmutableComplexNumber.imaginary, 2)
assertEquals(thatImmutableComplexNumber.real, 3)
assertEquals(thatImmutableComplexNumber.imaginary, 4)
}}Tool: REPL
Functional programming is a bit like using a calculator.
An interactive shell (or REPL, for Read-Eval-Print-Loop) lets one write expressions and responds with their value. Alternatively, you can use a scala worksheet.
Doc
REPL: https://docs.scala-lang.org/overviews/scala-book/scala-repl.html
Scala worksheet: https://docs.scala-lang.org/scala3/book/tools-worksheets.html
Example
The Scala REPL can be started by simply typing
> scalaHere are some simple interactions with the REPL
scala> 87 + 145
res0: Int = 232 Functional programming languages are more than simple calcululators because they let one define values and functions:
scala> def size = 2
size: Int
scala> 5 * size
res1: Int = 10Elements of Programming
Every non-trivial programming language provides:
- primitive* expressions representing the simplest elements
- ways to combine expressions
- ways to abstract expressions, which introduce a name for an expression that can be referred to.
Primitive
In Scala, Primitive types are similar to Java but are written capitalized:
| Int | 32-bit integers |
|---|---|
| Long | 64-bit integers |
| Float | 32-bit floating-point numbers |
| Double | 64-bit floating-point numbers |
| Char | 16-bit Unicode characters |
| Short | 16-bit integers |
| Byte | 8-bit integers |
| Boolean | boolean values true and false |
Evaluation
A non-primitive expression is evaluated as follows.
- Take the leftmost operator
- Evaluate its operands (left before right)
- Apply the operator to the operands
A name is evaluated by replacing it with the right-hand side of its definition.
The evaluation process stops once it results in a value.
Example: Circumference

// Circumference
def pi = 3.14159
def radius = 10
(2 * pi) * radiusScala worksheet output
def pi: Double
def radius: Int
val res0: Double = 62.8318Parameters
Definitions can have parameters.
def square(x: Double) = x * x
square(2)
square(5 + 4)
square(square(4)) Output
def square(x: Double): Double
val res0: Double = 4.0
val res1: Double = 81.0
val res2: Double = 256.0
Function parameters come with their type, which is given after a colon.
def sumOfSquares(x: Double, y: Double) = square(x) + square(y) Applications of parameterized functions are evaluated similarly as operators:
- Evaluate all function arguments, from left to right
- Replace the function application by the function’s right-hand side, and, at the same time
- Replace the formal parameters of the function with the actual arguments
sumOfSquares(3, 2+2)it is converted to
-> sumOfSquares(3, 4)
-> square(3) + square(4)
-> 9 + 16Output
def sumOfSquares(x: Double, y: Double): Double
val res3: Double = 25The substitution Model
Function Termination
Q: Does every expression reduce to a value (in a finite number of steps)?
No. Here is a counter-example
def loop: Int = loop loopSubstitution Model
This scheme of expression evaluation is called the substitution model, where
- all evaluation does is reduce an expression to a value.
- It can be applied to all expressions, as long as they have no side effects (storing files, printing, reading etc.).
- The substitution model is formalized in the
λ-calculus, which gives a foundation for functional programming.
Functional Contract
- A method with a functional contract will always return the same value to the same arguments.
- Have no other side effects (like storing files, printing, reading).
-
Thus, even if you mutate temporary values inside your function, it is still pure from the outside.
Call-by-Name and Call-by-Value
Call-by-Value
The interpreter reduces function arguments to values before rewriting the function application.
def square(x: Double ) = x * x
def sumOfSquares(x: Double, y: Double) = square(x) + square(y)
sumOfSquares(3, 2+2)
square(3) + square(2+2)
3 * 3 + square(2+2)
9 + square(2+2)
9 + (2+2) * (2+2)
9 + 4 * (2+2)
9 + 4 * 4
25Call-by-Name
Apply the function to unreduced arguments.
We prepend => (rocket symbol) to its type.
def callByNameFunc(input: => InputType) def square(x: => Double ) = x*x
def sumOfSquares(x: => Double, y: => Double) = square(x) + square(y)
sumOfSquares(3, 2+2)
sumOfSquares(3, 4)
square(3) + square(4)
3 * 3 + square(4)
9 + square(4)
9 + 4 * 4
9 + 16
25Comparison
Both strategies reduce to the same final values as long as
- the reduced expression consists of pure functions, and
- both evaluations terminate.
Performance
Say we have a function that takes two inputs and returns the square of the first input
i.e. the 2nd input is not used
def squareOfFirstElement(x: Int, y: Int) = x * xWhich one is faster? Call by name or call by value?
squareOfFirstElement(7, 8)
squareOfFirstElement(3+4, 8)
squareOfFirstElement(7, 2*4)
squareOfFirstElement(3+4, 2*4) We want to examine the evaluation strategy and determine which one is faster (fewer steps) in these conditions:
Scenario 1
squareOfFirstElement(2,3)call by value:
squareOfFirstElement(2,3)
↓
2*2
↓
4 call by name:
squareOfFirstElement(2,3)
↓
2*2
↓
4 Here the result is reached with the same number of steps.
Senario 2
squareOfFirstElement(3+4,8)call by value:
squareOfFirstElement(7,8)
↓
7*7
↓
49 call by name:
(3+4)*(3+4)
↓
7*(3+4)
↓
7*7
↓
49 Here call by value is faster.
Senario 3
squareOfFirstElement(7,2*4)call by value:
squareOfFirstElement(7,8)
↓
7*7
↓
49call by name:
7 * 7
↓
49 Here call by name is faster.
Senario 4
squareOfFirstElement(3+4, 2*4) call by value:
squareOfFirstElement(7,2*4)
↓
squareOfFirstElement(7, 8)
↓
7*7
↓
49 call by name:
(3+4)*(3+4)
↓
7*(3+4)
↓
7*7
↓
49 The result is reached within the same steps.
Advantage
Call-by-value
- it evaluates every function argument only once
- avoids the repeated re-computation of argument expressions
Call-by-name
- a function argument is not evaluated if the corresponding parameter is unused in the evaluation of the function body.
Termination
Call-by-name and call-by-value evaluation strategies reduce an expression to the same value as long as both evaluations terminate.
Q: But what if termination is not guaranteed?
If CBV evaluation of an expression #e terminates, then CBN evaluation of #e terminates, too.
The other direction is not true.
| Terminates? | CallByName | CallByValue | Possible? |
|---|---|---|---|
| 1 | T | T | T |
| 2 | F | T | F |
| 3 | F | F | T |
| 4 | T | F | T |
For example: find an expression that terminates under CBN but not under CBV.
def firstByValue(x: Int, y: Int) = x
def firstByName(x: => Int, y: => Int) = x
def loop: Int = {
while (true) {
Thread.sleep(1000)
}
1
}
// #loop never called,
firstByName(1, loop)
// Return: val res0: Int = 1
// Whill try to exe #loop first
firstByValue(1, loop)
// Never end